To illustrate the capabilities and performance of the parallel adaptive load-balancing framework, the results of 3D analysis of Anchor pullout test are presented. In this example, h-adaptive analysis has been used together with heuristic error indicator based on attained damage level. The PETSc[1] (solution of the linearized system) and ParMETIS[2] ((re)partitioning) libraries have been used. Both examples have been computed using the OOFEM solver.
In order to assess the behavior and performance of the proposed methodology, the case study analyzes were run without the dynamic load balancing (static partitioning was employed, marked as ``nolb'') and with dynamic load balancing performed before (``prelb'') or after (``postlb'') the error assessment.
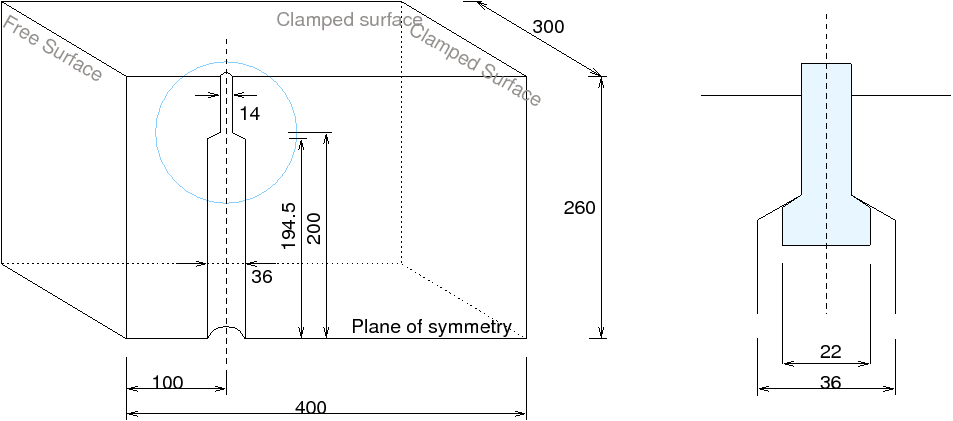
The geometry and setup of the test are shown in Fig 1. The anchor is located close to the boundary, requiring full 3D analysis with only one plane of symmetry. As the steel anchor is pulled out of concrete, the crack surface is initiated at the anchor head and starts to propagate towards the boundary as the loading increases. To model concrete fracture, an anisotropic, non-local damage based model has been used. The original mesh consists of 16772 linear tetrahedral elements and 1456 nodes, which was subsequently refined in 20 steps into a final mesh with 125400 elements and 22441 nodes. For the solution of the linearized system, PETSc library has been used (sparse, coordinate based storage scheme (compressed row format), conjugate gradient iterative solver with incomplete Cholesky preconditioner).
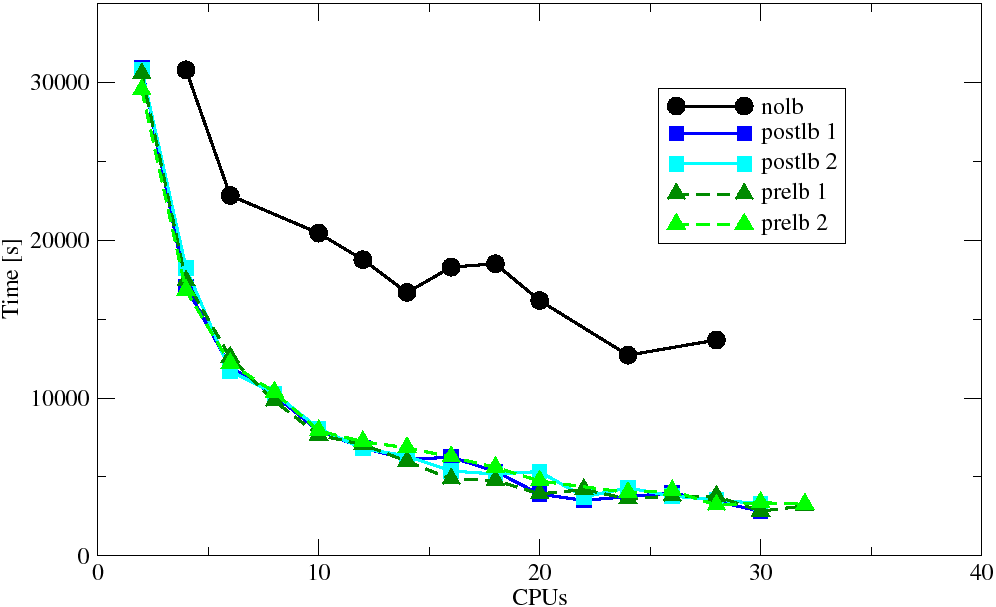
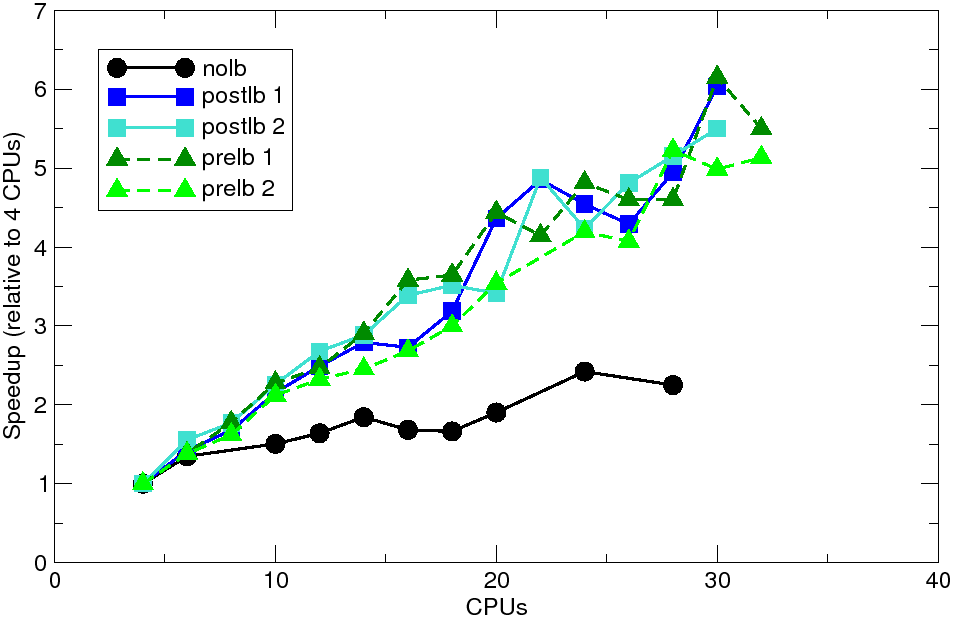
The problem has been solved on SGI Altix 4700 machine installed at CTU computing centre. Similarly to previous example, to assess the behaviour and performance of the proposed methodology, the case study analyzes were run without the dynamic load balancing (static partitioning was employed) and with dynamic load balancing performed before or after the error assessment. The obtained solution times (averaged over two or three analysis runs) and corresponding speedups (relative to 4 CPUs) are summarized in Figure 2.
| Fig. 2: Anchor pullout test: solution times and speedups on SGI Altix | |
 |
 |
The achieved results reveal that the effect of the dynamic load balancing is quite substantial. When no load balancing is applied the solution times are decreasing with the number of CPUs only slightly, which is the direct consequence of heavy imbalance due to the localized refinement resulting in dramatic increase of number of elements in one or a few subdomains. With the dynamic load balancing, this effect is alleviated. The obtained speedup of the load-balanced computation is showing clear linear trend, indicating a very good scalability of the parallel agorithm. Also, the absolute values of attained speedups are very good.
More details can be found in [3] and [4].
[1] Satish Balay and Kris Buschelman and William D. Gropp and Dinesh Kaushik and Matthew G. Knepley and Lois Curfman McInnes and Barry F. Smith and Hong Zhang: PETSc Web page, http://www.mcs.anl.gov/petsc, 2009.
[2] ParMETIS - Parallel Graph Partitioning and Fill-reducing Matrix Ordering, http://glaros.dtc.umn.edu/gkhome/metis/parmetis/overview.
[3] B. Patzák and D. Rypl. Parallel adaptive finite element computations with dynamic load balancing. In B. H. V. Topping, L. F. Costa Neves, and R. C. Barros, editors, Proceedings of the Twelfth International Conference on Civil, Structural and Environmental Engineering Computing, Stirlingshire, United Kingdom, 2009. Civil-Comp Press. paper 114.
[4] B. Patzák and D. Rypl. A framework for parallel adaptive finite element computations with dynamic load balancing. In B. H. V. Topping, editor, CD-ROM Proceedings of the First International Conference on Parallel, Distributed and Grid Computing for Engineering, Pecs, Hungary, 2009. Civil-Comp Press. ISSN: 1759-3433, ISBN: 978-1-905088-29-4.
| This page is part of the OOFEM project
documentation (www.oofem.org) (c) 2008 Borek Patzak, e-mail: info(at)oofem(dot)org |

|