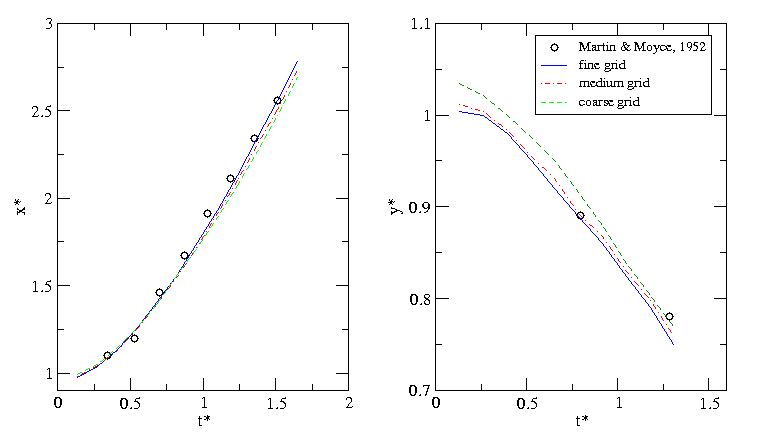
Fig. 2: Broken dam problem - the position of the wave front (left) and the height of residual column (right) as function of time. Comparison with experimental results
Eulerian formulation is adopted, which is typically used in CFD applications. The numerical solution is based on stabilized finite element method (SUPG/PSPG) and interface-capturing method based on VOF approach to track the position of free surface [2]. Recently, level set based representation has been implemented. The advantage of the above approaches is the fact that they can implicitly handle topological changes of interface geometry, including the breakup and coalescence of fluid masses.
In order to verify the VOF interface tracking algorithm, a broken dam
problem has been analyzed.
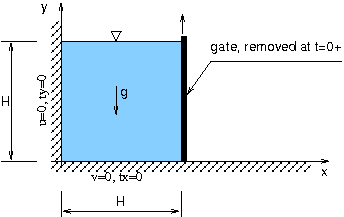
The setup of the experiment is illustrated in
Fig. 1. A rectangular column in hydrostatic
equilibrium is confined by a vertical wall and the gate. The gate is
suddenly removed and the water column starts to collapse due to its
gravity by forming advancing water wave. An initial configuration is
chosen as a square water column (H=0.05175m), following the experimental
setup by Martin & Moyce [1]. Frictionless boundary
conditions are assumed on bottom and vertical walls. The density and
viscosity of water are taken as 1000 [kg/m^3] and 1x10^-3 [Pa.s]. The
ambient air with density equal to 1 [kg/m^3] and viscosity 1x10^-5 [Pa.s]
is assumed. Three different discretizations with 1020, 4080, and 16320
elements have been used to verify
the objectivity of the description with respect to mesh size.
The position of water front and residual water column height with
respect to time are compared to experimental results in
Fig. 2. For convenience, the dimensionless length
x*=x/H and time t*=t*sqrt(g/H) are used in this figure. In
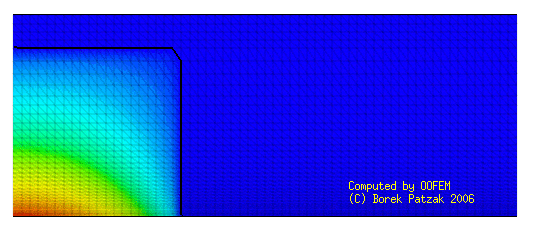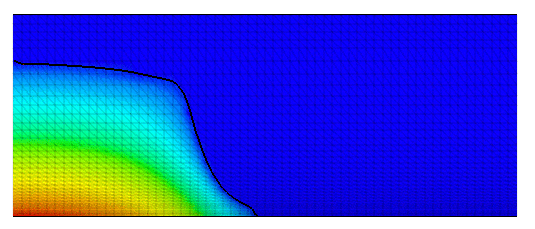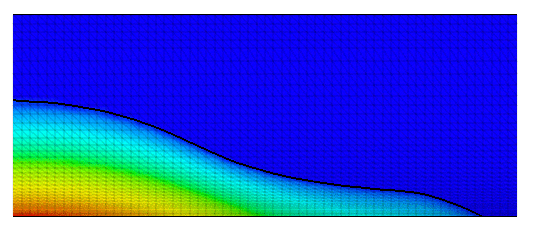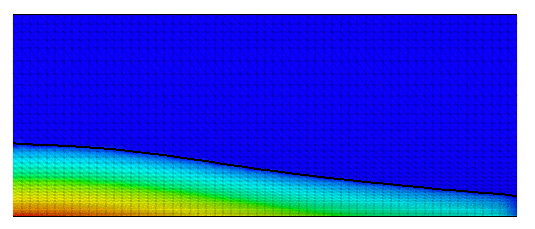
Fig. 3 the position and pressure contours are shown
for different stages of solution process.

Fig. 2: Broken dam problem - the position of the wave front (left) and
the height of residual column (right) as function of
time. Comparison with experimental results
| Fig. 3: Broken dam problem - Animation of free surface evolution with pressure contours | Fig. 4: Broken dam problem - Animation of free surface evolution with velocity field |
 |
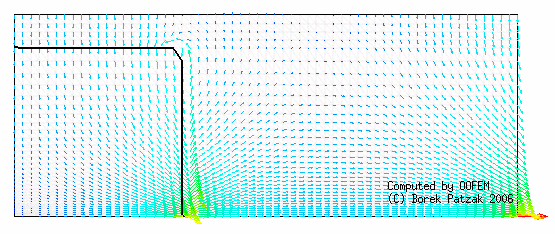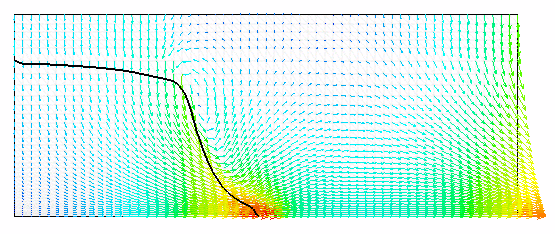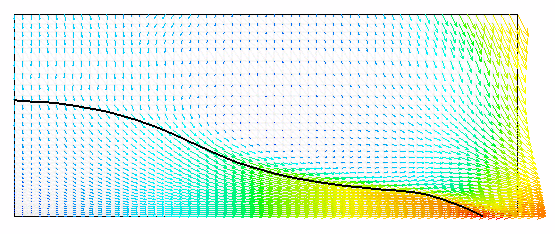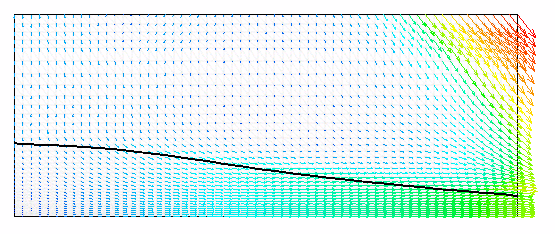 |
Recently, a level set based interface-capturing approach has been developed to track the position of a free surface on general, triangulated, unstructured meshes. The interface is defined as a zero level set of a suitable higher-dimensional function (called level set function). For example, in two dimensions, the level set method represents given curve in the plane as the zero level set of a two-dimensional auxiliary function, usually defined as signed distance function. The interface is not manipulated directly, it is manipulated implicitly through the level set function. The advantages of this approach consist in natural handling of topological changes and straight forward generalization into multiple dimensions. The algorithm is based on explicit positive coefficient scheme (see Barth and Sethian [3]) together with reinitialization technique to maintain signed distance property of level set representation. The following figures illustrate the evolution of level set representation for different solution steps, the isocontours of level set function are shown, as well as zero level set representing the interface (black line)
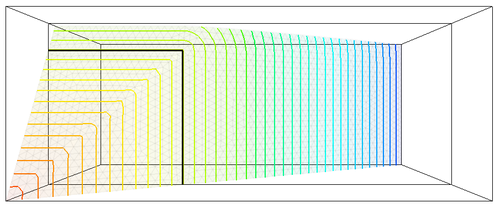 |
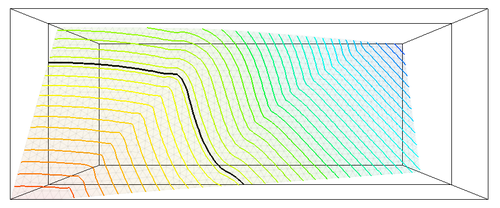 |
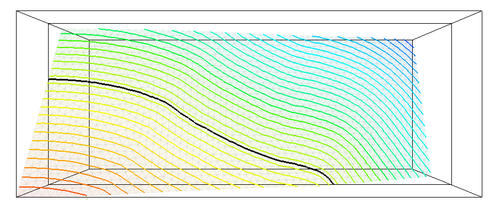 |
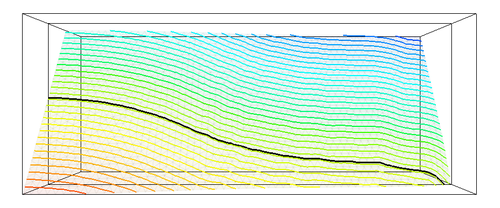 |
[1] Martin JC, Moyce WJ.: An Experimental
study of the collapse of liquid columns on a rigid horizontal
plane. Philosophical Transactions of the Royal Society of London,
Series A. Mathematical, Physical and Engineering Sciences:1952;
244:312-324.
[2] B. Patzák and Z. Bittnar. Simulation of fresh concrete flow. In B. H. V. Topping, G. Montero, and R. Montenegro, editors, Proceedings of the Fifth International Conference on Engineering Computational Technology, Stirlingshire, United Kingdom, 2006. Civil-Comp Press. paper 204.
[3] T.J. Barth, J.A. Sethian. Numerical Schemes for the Hamilton-Jacobi and Level Set Equations on Triangulated Domains, J. Comp. Phys., 145, 1, pp. 1--40, 1998.
| This page is part of the OOFEM project
documentation (www.oofem.org) (c) 2008 Borek Patzak, e-mail: info(at)oofem(dot)org |

|