To illustrate the capabilities and performance of the parallel adaptive load-balancing framework, the results of 2D analysis of Brazilian splitting test are presented. In this example, h-adaptive analysis has been used together with heuristic error indicator based on attained damage level. The PETSc[1] (solution of the linearized system) and ParMETIS[2] ((re)partitioning) libraries have been used. Both examples have been computed using the OOFEM solver.
In order to assess the behavior and performance of the proposed methodology, the case study analyzes were run without the dynamic load balancing (static partitioning was employed, marked as ``nolb'') and with dynamic load balancing performed before (``prelb'') or after (``postlb'') the error assessment.
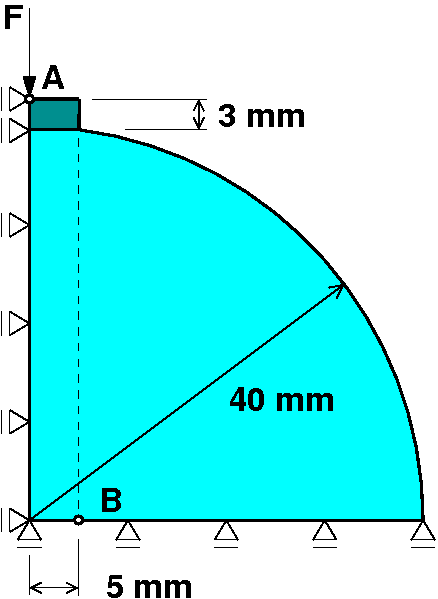
This test is a standard technique for determination of the tensile strength of concrete. A cylindrical specimen is loaded along its vertical diametral plane. The compressive load, transferred to the specimen via steel bearing plates at the top and bottom sides, induces tension stress in the horizontal direction leading finally to the rupture of the specimen along the loading plane. Due to the double symmetry, the analysis itself is performed only on the quarter of the specimen under plain strain conditions. The concrete behavior is described by the nonlocal scalar damage model, while the steel bearing plates are assumed to be linearly elastic. The nonlinear problem was solved incrementally in 40 time steps. During the solution the initial coarse mesh consisting of 220 elements was gradually refined up to 8763 elements.
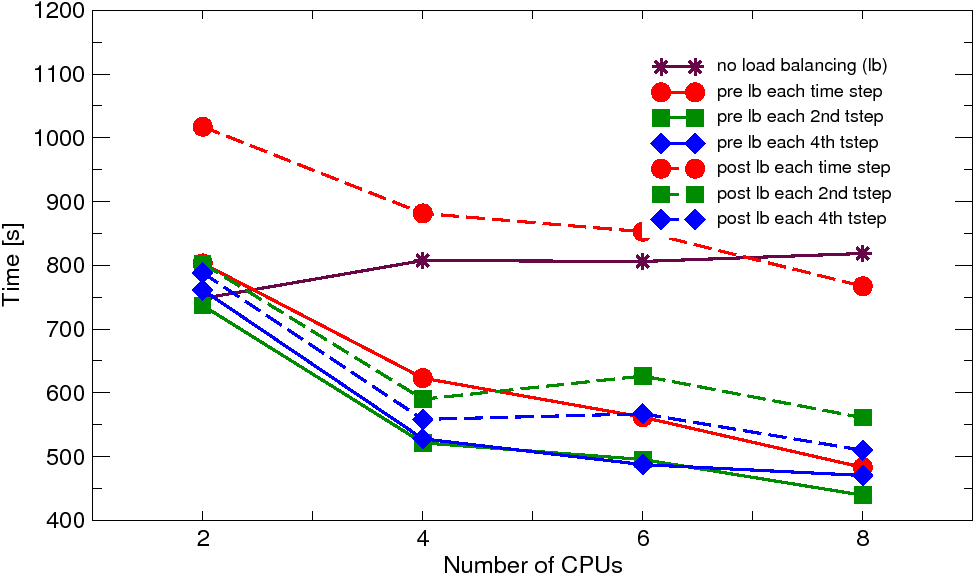
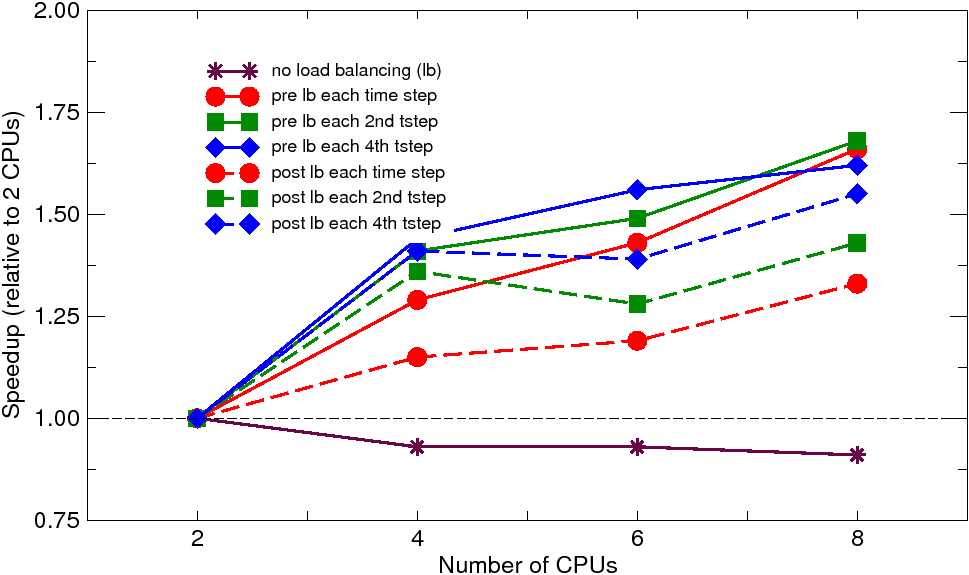
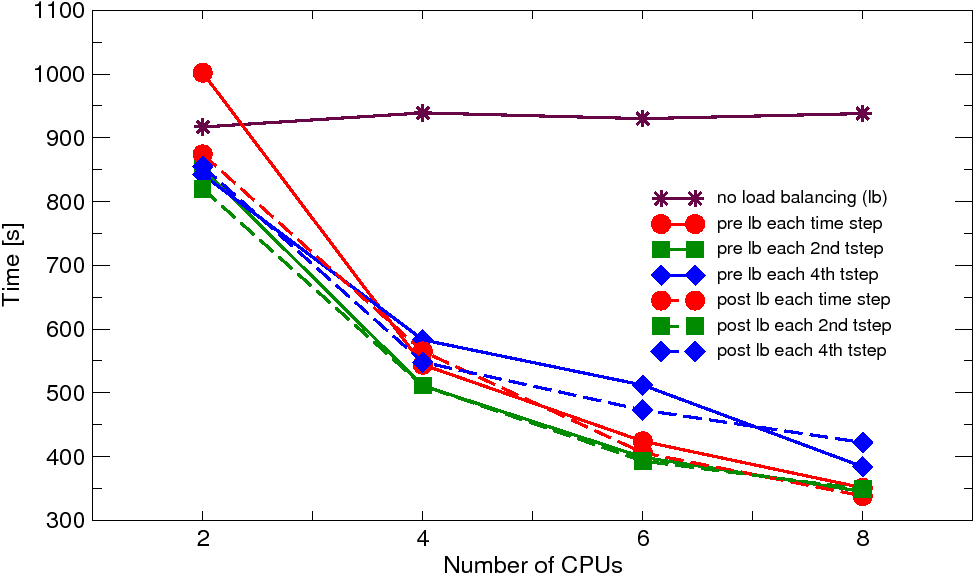
The problem has been solved on workstation cluster composed of office-based PCs (Dell Optiplex) with single core CPUs at 3.4 GHz, interconnected by gigabit ethernet and on SGI Altix 16-node machine with dual core CPUs running at 1.3 and 1.5 GHz, interconnected by the NUMAflex architecture (NUMAlink 3 with 3.2 GB/s and NUMAlink 4 with 6.4 GB/s bidirectionally). Parallel nonlinear adaptive simulations have been performed using 2, 4, 6, and 8 processors. In each run with the dynamic load balancing, the balancing was enforced either at each time step or at each second or fourth time step. The obtained solution times (averaged over two or three analysis runs) and corresponding speedups (relative to 2 CPUs) are summarized in Figures 2 and 3.
| Fig. 2: Brazilian test: solution times and speedups on workstation cluster | ||
 |
 |
|
| Fig. 3: Brazilian test: solution times and speedups on SGI Altix | |
 |
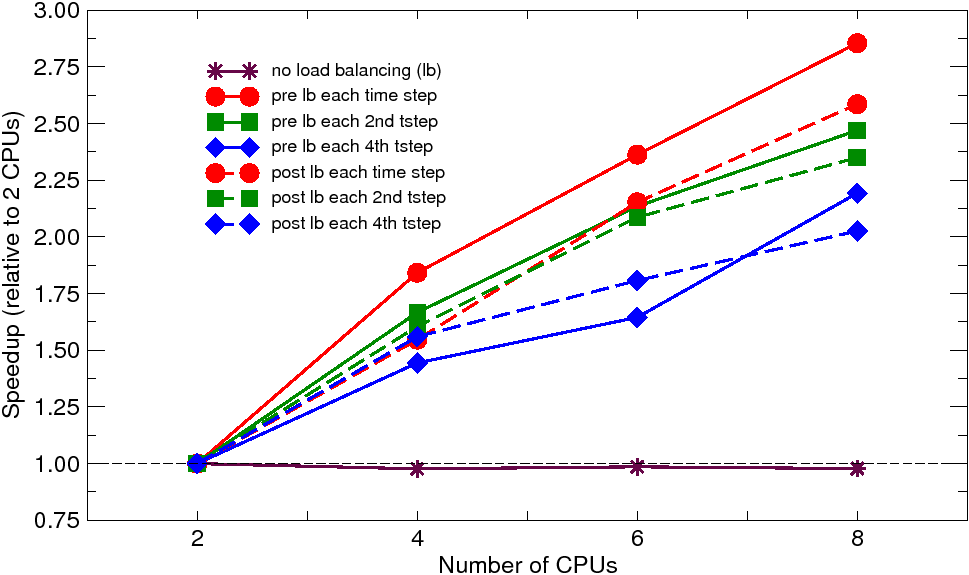 |
The results on cluster reveal quite poor scalability. On the other hand, the effect of the dynamic load balancing is quite apparent. When no load balancing is applied the solution times are slightly increasing with the number of CPUs, which is the direct consequence of heavy imbalance due to the localized refinement (five levels of subdivision in the fracture process zone were necessary) resulting in dramatic increase of number of elements in one or a few subdomains. With the dynamic load balancing, this effect is alleviated, which results in some speedup. The dynamic load balancing applied before the adaptive remeshing performs generally better than that performed after the remeshing. This indicates that the cost of the rebalancing on the adaptively refined mesh is relatively large compared to the gain that the next time step is solved on the balanced refined mesh. Note, that for such a small-scale analysis the communication cost (further increased by nonlocality of the used material model) is clearly the dominating factor. The same analysis on SGI Altix reveals much better scalability and attained speedups, caused by much faster communication on this platform, compared to the workstation cluster.
More details can be found in [3] and [4].
[1] Satish Balay and Kris Buschelman and William D. Gropp and Dinesh Kaushik and Matthew G. Knepley and Lois Curfman McInnes and Barry F. Smith and Hong Zhang: PETSc Web page, http://www.mcs.anl.gov/petsc, 2009.
[2] ParMETIS - Parallel Graph Partitioning and Fill-reducing Matrix Ordering, http://glaros.dtc.umn.edu/gkhome/metis/parmetis/overview.
[3] B. Patzák and D. Rypl. Parallel adaptive finite element computations with dynamic load balancing. In B. H. V. Topping, L. F. Costa Neves, and R. C. Barros, editors, Proceedings of the Twelfth International Conference on Civil, Structural and Environmental Engineering Computing, Stirlingshire, United Kingdom, 2009. Civil-Comp Press. paper 114.
[4] B. Patzák and D. Rypl. A framework for parallel adaptive finite element computations with dynamic load balancing. In B. H. V. Topping, editor, CD-ROM Proceedings of the First International Conference on Parallel, Distributed and Grid Computing for Engineering, Pecs, Hungary, 2009. Civil-Comp Press. ISSN: 1759-3433, ISBN: 978-1-905088-29-4.
| This page is part of the OOFEM project
documentation (www.oofem.org) (c) 2008 Borek Patzak, e-mail: info(at)oofem(dot)org |

|