Problem representation (Engineering model)

In this section, we introduce in detail how the problems are represented, their discrete form assembled and finally solved.

We start with EngngModel class, which is an abstraction for the problem under consideration. It represents the analysis to be performed. Base class declares and implements the basic general services for assembling characteristic components and services for starting the solution step and its termination. Derived classes know the form of governing equation and the physical meaning of particular components. They are responsible for forming the governing equation for each solution step, usually by summing contributions from particular elements and nodes, and their solution using the suitable numerical method.

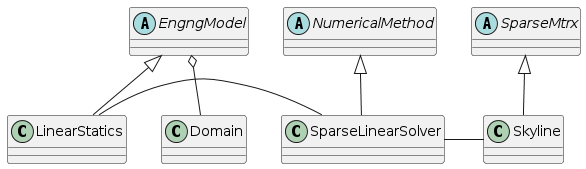
The solution step may represent either a time step, a load increment, or a load case. The solution steps are grouped together into so called meta steps. The meta step can be thought as a sequence of solution steps, with the same set of attributes used to drive the behavior of EngngModel. For each meta step, the EngngModel typically updates its control parameters according to ones defined by meta step (see updateAttributes service) and generates the sequence of the solution steps. This allows to switch to a different time increment, a different solution control, etc. If no meta step is specified, the EngngModel creates a default one for all solution steps. There are two services, where EngngModel attributes are set or updated. The first one, used for those attributes which do not vary during the solution of the problem, are initialized in instanciateYourself service. The updateAttributes method is called when specific meta step is activated, and selected attributes are updated from corresponding meta step attributes. If no meta step is introduced, a default one is created (with the attributes set to the EngngModel attributes). Then there is no difference, whether the attributes are initialized in instanciateYourself or in updateAttributes, but the preferred scheme is to read all attributes in instanciateYourself and to left updateAttributes service empty.

The basic EngngModel tasks are following:

• Assembling governing equations by summing contributions (typically from nodes and elements).

• Solving the problem described by governing equation(s) using the instance of a suitable numerical method. This requires to establish a mapping between numerical method-parameters and EngngModel components of governing equation. EngngModel must map each component of governing equation(s) (which has physical meaning) to the corresponding numerical component. This mapping between physical components to independent numerical components (understood by the numerical method) is important, because it allows the numerical method to be used by many EngngModels with different component meaning and allows to use different numerical methods by EngngModel. This is achieved by using the compulsory numerical component names (see further).

• Providing access to the problem solution. Services for returning unknown values according to their type and mode are provided. These services are used by DOFs to access their corresponding unknowns.

• Terminating the time step by updating the state of the problem domains (nodes and elements, including integration points).

• Managing the problem domains, meta steps, and problem input/output streams.

• Equation numbering.

• Storing and restoring problem state to/from context file.

• Managing and updating unknowns

The complete listing of EngngModel class declaration can be found here: https://github.com/oofem/oofem/blob/master/src/core/engngm.h. It is well commented and should be self-explanatory.

One of the key methods of EngngModel class is solveYourself, which is invoked to starts the solution of the problem. The default implementation loops over individual metasteps. For each metastep, the loop over nested solution steps is performed. The representation of solution step (TimeStep class instance) is created inside giveNextStep service and stored in EngngModel attribute currentStep. After some initializations, the solution step is solved by calling solveYourselfAt service, which performs solution for specific solution step, passed as its parameter.

The simplified implementation of solveYourself service is shown below:

void
EngngModel :: solveYourself ()
{
     int imstep, jstep;
     int smstep=1, sjstep=1;
     MetaStep* activeMStep;

     for (imstep = smstep; imstep<= nMetaSteps; imstep++) {
         activeMStep = this->giveMetaStep(imstep);
         for (jstep = sjstep; jstep <= activeMStep->giveNumberOfSteps(); jstep++) {
         this->giveNextStep();
         // update attributes according to new meta step attributes
         if (jstep == sjstep) this->updateAttributes (this->giveCurrentStep());
         this->solveYourselfAt(this->giveCurrentStep());
         this->updateYourself( this->giveCurrentStep() );
         this->terminate( this->giveCurrentStep() );

     }
}

The solveYourselfAt method typically assembles characteristic matrices and vectors and solves the problem using the suitable numerical method. The implementation should be provided by derived classes implementing specific problem. (see section ref{Engngmodelexample} for an example). After finishing the solution for the given solution step, updateYourself service is called to update the state of all components. Finally terminate service is called.

The default implementation of updateYourself service loops over all problem domains and calls corresponding update service for all DOF managers and elements:

void
EngngModel :: updateYourself(TimeStep *tStep)
{
    for ( auto &domain: domainList ) {
        for ( auto &dman : domain->giveDofManagers() ) {
            dman->updateYourself(tStep);
        }
        for ( auto &elem : domain->giveElements() ) {
             elem->updateYourself(tStep);
        }
}

The terminate` service essentially prints the required outputs and optionally saves the context file (if required), so the solution can be restarted from this saved state later:

void
EngngModel :: terminate(TimeStep *tStep)
{
    exportModuleManager.doOutput(tStep);
    this->saveStepContext(tStep, CM_State | CM_Definition);
}

Both services are virtual, so they can be easily tailored to specific needs.

The EngngModel class comes with handy generic services for characteristic components assembly, that are used by derived classes to assemble the characteristic components of the problem. They essentially loop over nodes or elements (depending on the character of the requested component) of the given domain, requesting the corresponding component (determined or even evaluated by assembler class instance) and corresponding code numbers. The component contributions are assembled (using code numbers) into a target array or matrix. Here we show the simplified implementation of one of these services to assemble the characteristic matrix:

void EngngModel :: assemble(SparseMtrx &answer, TimeStep *tStep, const MatrixAssembler &ma,
                            const UnknownNumberingScheme &s, Domain *domain)
{
    IntArray loc;
    FloatMatrix mat, R;
    int nelem = domain->giveNumberOfElements();

    for ( int ielem = 1; ielem <= nelem; ielem++ ) {
        auto element = domain->giveElement(ielem);
        ma.matrixFromElement(mat, *element, tStep);

        if ( mat.isNotEmpty() ) {
            ma.locationFromElement(loc, *element, s);
            if ( element->giveRotationMatrix(R) ) {
                mat.rotatedWith(R);
            }
            if ( answer.assemble(loc, mat) == 0 ) {
                OOFEM_ERROR("sparse matrix assemble error");
            }
        }
    }
}

The assemble service is used to assemble the characteristic matrix from elements contributions. The MatrixAssembler class instance is used to parametrize the aasemble method and it determines the element contributions. In the simple form, it can request characteristic matrix directly from element, but it can also evaluate the element contribution. The UnknownNumberingScheme class instance determines the unknown numbering and thus determines the code numbers of the unknowns. The SparseMtrx class instance is used to store the assembled matrix.

Numerial Method Interface

The EngngModel needs to solve the underlying discrete problem. This is done by the suitable instance of NumericalMethod class. The design attempts to separate the problem formulation from the numerical solution of the problem, and the data storage format.

Derived classes from NumericalMethod class are supposed to declare the interface for specific problem type (like solution of linear system). The interface usually consist in declaring virtual abstract function solve, with parameters corresponding to problem under consideration. The data are specified using parameters passed to solve method (so called mapping of physical components to their numerical counterpart). The parameters of numerical method either are passed to solve method or are set by instanciateYourself service from input file. The solve method shoud return value of NM_Status type.

Many problems require updating components during the solution. To keep definition and implementation of numerical method independent on particular problem, the EngngModel must also provide service for updating mapped components components, if this is necessary. This is provided by EngngModel::updateComponent method. This method is invoked by numerical method, when the update of some components during solution is needed (for example in the Newton Raphson algorithm for the solution of non-linear equations, stiffness or internal force vector need to be updated during the solution process).

The derived classes from class{Numerical method} are supposed to declare the interface for specific problem type (like solution of linear system). It should be pointed out, that all numerical methods solving the same numerical problem have to use the same genaral interface - this is enforced by introducing the abstract class representing family of numerical method for solving specific problem and declaring the common interface.

There are typically multiple numerical methods for solving the same problem. The NumericalMethod can implement the solution itself, but it can also implement an interface to external numerical libraries (like PETSc, Trilinos, etc.).

This concept is further enhanced by the introduction of a base abstract class SparseMatrix representing sparse matrix storage. This class only declares the basic required services provided by all sparse matrix implementations (like assembly of contribution, multiplication by a vector, possible factorization, etc). The implementation is left on derived classes. Numerical methods are then implemented only using basic services declared by the Sparse Matrix class. Thus, numerical method class instances will work with any sparse matrix representation, even added in the future, without changing any code.

As an example, the declaration of the SparseLinearSystem class is shown below. This class is an abstraction for all numerical methods solving sparse linear system of equations.

class SparseLinearSystemNM : public NumericalMethod
{
public:
    /// Constructor.
    SparseLinearSystemNM(Domain * d, EngngModel * m);
    /// Destructor.
    virtual ~SparseLinearSystemNM();

    /**
    * Solves the given sparse linear system of equations @f$ A\cdot x=b @f$.
    * @param A Coefficient matrix.
    * @param b Right hand side.
    * @param x Solution array.
    * @return Status of the solver.
    */
    virtual ConvergedReason solve(SparseMtrx &A, FloatArray &b, FloatArray &x) = 0;

    /**
    * Solves the given sparse linear system of equations @f$ A\cdot X=B @f$.
    * Default implementation calls solve multiple times.
    * @param A Coefficient matrix.
    * @param B Right hand side.
    * @param X Solution matrix.
    * @return Status of the solver.
    */
    virtual ConvergedReason solve(SparseMtrx &A, FloatMatrix &B, FloatMatrix &X);
};

To summarize, the natural independence of the problem formulation, numerical solution of the problem, and data storage format have been obtained, which leads to a modular and extensible structure.

Domain class

The computational grid is represented by Domain class. It manages all components of the FEM discrete model. These include dof managers (nodes, element sides possessing DOFs), elements, material and cross section models, boundary and initial conditions, time functions, and so on. For every component type Domain maintains the component list and provides the corresponding access services.

The basic services provided by Domain are the following:

• Reading its description from input and creating corresponding objects. This task includes the reading and parsing the particular mesh input records, creating the corresponding components representations (objects) of appropriate type, initializing these components using their instanciteFromString methods and storing them into corresponding list.

• Provides services for accessing its particular components. The services returning the total number of particular domain components and particular component access methods based on component number are provided.

The domain also manages instances of SpatialLocalizer and connectivityTable classes to serve the connectivity and spatial localization related services (finding elements shared by the node, finding the closest node search, finding the element containing given point, etc.).

For complete definition of Domain class interface, please go to https://github.com/oofem/oofem/blob/master/src/core/domain.h

Example - Linear Static Analysis implementation

In this section, the example of the implementation of linear static analysis will be given. The linear static analysis is a typical example of a structural engineering problem. In this particular case, the analysis is time independent, meta steps are not used (default one is created) and time steps are used to distinguish load cases (different load vectors).

The class definition includes the declaration of characteristic components of the problem - the stiffness matrix and load and displacement vectors. Two additional variables are used to store the linear solver type and the sparse matrix type, which can be selected by the user. Finally, the reference to suitable instance of SparseLinearSystemNM class is stored in the nMethod attribute.

The following services are declared/implemented:

• solveYourselfAt for solving the solution step, responsible for forming the stiffness matrix and load vector, and calling the numerical method to solve the problem,

• giveUnknownComponent providing access to problem unknowns (displacements),

• context i/o services for serializing and deserializing the state of the problem (saveContext and restoreContext services),

• solver parameter initialization (initializeFrom) and consistency checking (checkConsistency).

class LinearStatic : public StructuralEngngModel
{
protected:
    std :: unique_ptr< SparseMtrx > stiffnessMatrix;
    FloatArray loadVector;
    FloatArray displacementVector;

    LinSystSolverType solverType;
    SparseMtrxType sparseMtrxType;
    /// Numerical method used to solve the problem.
    std :: unique_ptr< SparseLinearSystemNM > nMethod;

    int initFlag;
    EModelDefaultEquationNumbering equationNumbering;

public:
    LinearStatic(int i, EngngModel *master = nullptr);
    virtual ~LinearStatic();

    void solveYourself() override;
    void solveYourselfAt(TimeStep *tStep) override;

    double giveUnknownComponent(ValueModeType type, TimeStep *tStep, Domain *d, Dof *dof) override;
    void saveContext(DataStream &stream, ContextMode mode) override;
    void restoreContext(DataStream &stream, ContextMode mode) override;

    void updateDomainLinks() override;

    TimeStep *giveNextStep() override;
    NumericalMethod *giveNumericalMethod(MetaStep *mStep) override;

    void initializeFrom(InputRecord &ir) override;

    virtual UnknownNumberingScheme &giveEquationNumbering() { return equationNumbering; }

    // identification
    virtual const char *giveInputRecordName() const { return _IFT_LinearStatic_Name; }
    const char *giveClassName() const override { return "LinearStatic"; }
};

The implementation of the class{LinearStatic} class and its methods follows. First, we start with initializeFrom method, responsible for reading user input parameters. The input record is represented by instance of InputRecord class, which allows for key-value lookup. The LinearStatic reads the solver type and sparse matrix type from the input record and stores them in the corresponding attributes. The error handling is achieved using exceptions thrown by IR_GIVE_OPTIONAL_FIELD macros, which is defined in the InputRecord class.

void
LinearStatic :: initializeFrom(InputRecord &ir)
{
    // call parent class
    StructuralEngngModel :: initializeFrom(ir);

    int val = 0;
    IR_GIVE_OPTIONAL_FIELD(ir, val, _IFT_EngngModel_lstype);
    solverType = ( LinSystSolverType ) val;

    val = 0;
    IR_GIVE_OPTIONAL_FIELD(ir, val, _IFT_EngngModel_smtype);
    sparseMtrxType = ( SparseMtrxType ) val;

}

The giveNumericalMethod method is responsible for allocating and returning the suitable instance numerical method. The method uses class factory to create the instance of the sparse linear solver.

NumericalMethod *LinearStatic :: giveNumericalMethod(MetaStep *mStep)
{
    if ( !nMethod ) {
        nMethod = classFactory.createSparseLinSolver(solverType, this->giveDomain(1), this);
    }
    if ( !nMethod ) {
        OOFEM_ERROR("linear solver creation failed for lstype %d", solverType);
    }
    return nMethod.get();
}

The giveUnknownComponent method provides access to problem unknowns, in our case to displacement vector. the unknown component of the problem. The method is called by the numerical method to access the unknowns (displacements) of the problem.

double LinearStatic :: giveUnknownComponent(ValueModeType mode, TimeStep *tStep, Domain *d, Dof *dof)
{
    // get DOF equation number
    int eq = dof->__giveEquationNumber();

    if ( tStep != this->giveCurrentStep() ) {
        OOFEM_ERROR("unknown time step encountered");
        return 0.;
    }

    switch ( mode ) {
    case VM_Total:
    case VM_Incremental:
        if ( displacementVector.isNotEmpty() ) {
            return displacementVector.at(eq);
        } else {
            return 0.;
        }

    default:
        OOFEM_ERROR("Unknown is of undefined type for this problem");
    }

    return 0.;
}

Finally, we provide the implementation of the solveYourselfAt method, which is responsible for solving the problem at the given time step representing load-case. The method first assembles the stiffness matrix and load vector, and then calls the numerical method to solve the problem.

void LinearStatic :: solveYourselfAt(TimeStep *tStep)
{
    // initFlag is used to avoid assembling stiffness matrix for each load-case
    if ( initFlag ) {
        OOFEM_LOG_DEBUG("Assembling stiffness matrix\n");
        stiffnessMatrix = classFactory.createSparseMtrx(sparseMtrxType);
        if ( !stiffnessMatrix ) {
            OOFEM_ERROR("sparse matrix creation failed");
        }

        stiffnessMatrix->buildInternalStructure( this, 1, this->giveEquationNumbering() );
        // use TangentAssembler to assemble the stiffness matrix
        this->assemble( *stiffnessMatrix, tStep, TangentAssembler(TangentStiffness),
                    this->giveEquationNumbering(), this->giveDomain(1) );
        initFlag = 0;
    }
    // allocate space for displacementVector
    displacementVector.resize( this->giveNumberOfDomainEquations( 1, this->giveEquationNumbering() ) );
    displacementVector.zero();
    loadVector.resize( this->giveNumberOfDomainEquations( 1, this->giveEquationNumbering() ) );
    loadVector.zero();

    OOFEM_LOG_DEBUG("Assembling load\n");
    this->assembleVector( loadVector, tStep, ExternalForceAssembler(), VM_Total,
                        this->giveEquationNumbering(), this->giveDomain(1) );

    // assemble internal part of load vector (forces induced by prescribed displacements, etc.)
    FloatArray internalForces( this->giveNumberOfDomainEquations( 1, this->giveEquationNumbering() ) );
    internalForces.zero();
    this->assembleVector( internalForces, tStep, InternalForceAssembler(), VM_Total,
                        this->giveEquationNumbering(), this->giveDomain(1) );

    loadVector.subtract(internalForces);

    OOFEM_LOG_INFO("\n\nSolving ...\n\n");

    this->giveNumericalMethod( this->giveMetaStep( tStep->giveMetaStepNumber() ) );
    ConvergedReason s = nMethod->solve(*stiffnessMatrix, loadVector, displacementVector);
    if ( s != CR_CONVERGED ) {
        OOFEM_ERROR("No success in solving system.");
    }
}

Please refer to full source code of the LinearStatic class in the OOFEM source code repository for more details: https://github.com/oofem/oofem/blob/master/src/sm/EngineeringModels/linearstatic.C

Problem representation (symbolic mode)

Starting from the version 3.0, OOFEM also supports symbolic mode allowing to define the problem by defining its weak form in terms of variables, terms, and integrals. The variables, terms and integrals are attributes of EngngModel class. In symbolic mode the governing equations are assembled from contributions of individual integrals, which are defined over specific domains (e.g. whole domain, boundary, etc.) and are composed of terms. The terms are defined in terms of variables. These variables can represent various physical quantities, such as displacements, temperatures, pressures, etc. In this mode, the elements do not define any physics, they just define the geometry; special family of elements is introduced for this purpose, allowing to parametrize the element geometry with different interpolations.

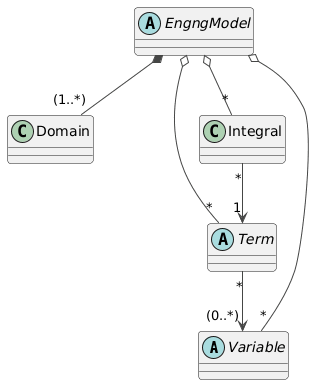
The assembly of the governing equations in symbolic mode by EngngModel is then performed by looping over all integrals, requesting the integral to assemble its contribution to the global system. The integrals in turn loop over their terms, requesting the term to assemble its contribution. The term then evaluates its contribution by using the variables it is defined with.

// assemble lhs
effectiveMatrix = classFactory.createSparseMtrx(sparseMtrxType);
effectiveMatrix->buildInternalStructure( this, 1, EModelDefaultEquationNumbering() );
if ( this->keepTangent ) {
    this->effectiveMatrix->zero();
    // loop over lhs integrals
    for (auto i: lhsIntegrals) {
        Integral* integral = this->integralList[i-1].get();
        integral->assemble_lhs (*effectiveMatrix, EModelDefaultEquationNumbering(), tStep);
    }
}

// assemble rhs
FloatArray rhs(this->giveNumberOfDomainEquations( 1, EModelDefaultEquationNumbering() ));
// loop over rhs integrals
for (auto i: rhsIntegrals) {
    Integral* integral = this->integralList[i-1].get();
    integral->assemble_rhs (rhs, EModelDefaultEquationNumbering(), tStep);
}