Next: Anisotropic damage model - Up: Material models for tensile Previous: Isotropic damage model for
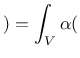
Instead
of averaging the equivalent strain, one can average the compliance variable
![]() , directly related to damage according to the formula
, directly related to damage according to the formula
![]() .
.
The weight function ![]() contains a certain parameter with the dimension
of length, which is in general called the characteristic length. Its specific
meaning depends on the type of weight function. The following functions are
currently supported:
contains a certain parameter with the dimension
of length, which is in general called the characteristic length. Its specific
meaning depends on the type of weight function. The following functions are
currently supported:
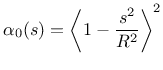
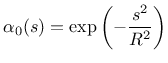
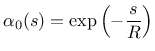
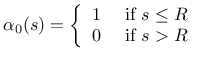
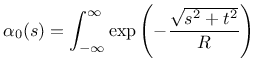 d
d
The above functions depend only on the distance ![]() between the interacting
points and are not normalized. If the normalizing
condition
between the interacting
points and are not normalized. If the normalizing
condition
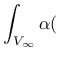
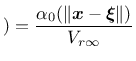
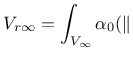
If the body of interest is finite (or even semi-infinite), the averaging
integral can be performed only over
the domain filled by the body, and the volume contributing to the nonlocal
average at a point
![]() near the boundary is reduced as compared to
points
near the boundary is reduced as compared to
points
![]() far from the boundary or in an infinite body. To make sure
that the normalizing condition
far from the boundary or in an infinite body. To make sure
that the normalizing condition
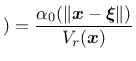
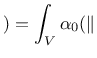
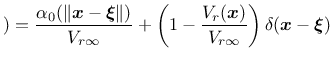
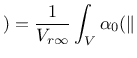
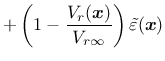
In a recent paper [11], special techniques that modify the averaging procedure based on the distance from a physical boundary of the domain or on the stress state have been considered. The details are explained in [11]. These techniques can be invoked by setting the optional parameter nlVariation to 1, 2 or 3 and specifying additional parameters ![]() and
and ![]() for distance-based averaging, or
for distance-based averaging, or ![]() for stress-based averaging.
for stress-based averaging.
The model parameters are summarized in Tabs. 24 and 25.
|
Borek Patzak