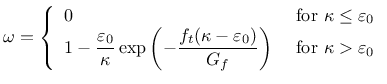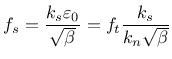Isotropic damage model for interfaces
The model provides an interface law which can be used to describe a damageable interface between two materials (e.g. between steel reinforcement and concrete). The law is formulated in terms of the traction vector and the displacement jump vector. The basic response is elastic, with stiffness kn in
the normal direction and ks in the tangential direction.
Similar to other isotropic damage models, this model assumes that the stiffness degradation is isotropic, i.e., both stiffness moduli decrease proportionally and independently of the loading
direction. The damaged stiffnesses are kn
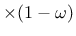 and ks
and ks
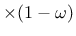 where
where 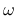 is a scalar damage variable.
The damage evolution law is postulated in an explicit form, relating
the damage variable
is a scalar damage variable.
The damage evolution law is postulated in an explicit form, relating
the damage variable 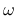 to the largest previously reached
equivalent “strain” level,
to the largest previously reached
equivalent “strain” level, 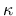 .
.
The equivalent “strain”,
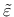 , is a scalar measure of the displacement jump vector. The choice of the specific expression
for the equivalent strain affects the shape of the elastic domain
in the strain space and plays a similar role to the choice of a yield
condition in plasticity.
Currently, in the present implementation, the equivalent strain is given by
, is a scalar measure of the displacement jump vector. The choice of the specific expression
for the equivalent strain affects the shape of the elastic domain
in the strain space and plays a similar role to the choice of a yield
condition in plasticity.
Currently, in the present implementation, the equivalent strain is given by
where
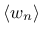 is the positive part of the normal displacement jump (opening of the interface)
and
is the positive part of the normal displacement jump (opening of the interface)
and 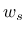 is the norm of the tangential part of displacement jump (sliding of the interface). Parameter
is the norm of the tangential part of displacement jump (sliding of the interface). Parameter 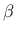 is optional and its default value is 0, in which case damage depends on the opening only (not on the sliding).
The dependence of damage
is optional and its default value is 0, in which case damage depends on the opening only (not on the sliding).
The dependence of damage 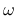 on maximum equivalent strain
on maximum equivalent strain 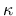 is described by the following damage
law which corresponds to exponential softening:
is described by the following damage
law which corresponds to exponential softening:
Here,
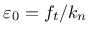 is the value of equivalent strain at the onset of damage.
Note that if the interface is subjected to shear traction only (with zero or negative normal traction),
the propagation of damage starts when the magnitude of the sliding displacement is
is the value of equivalent strain at the onset of damage.
Note that if the interface is subjected to shear traction only (with zero or negative normal traction),
the propagation of damage starts when the magnitude of the sliding displacement is
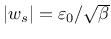 , i.e.,
when the magnitude of the shear traction is equal to
, i.e.,
when the magnitude of the shear traction is equal to
So the ratio between the shear strength and tensile strength of the interface, 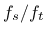 ,
is equal to
,
is equal to
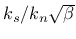 .
.
The model parameters are summarized in Tab. 28.
Table 28:
Isotropic damage model for interface elements - summary.
|
Description |
Isotropic damage model for concrete in tension |
|
Record Format |
isointrfdm01
kn(rn) # ks(rn) # ft(rn) # gf(rn) # [ maxomega(rn) #] talpha(rn) # d(rn) # |
|
Parameters |
- d material density |
|
|
- tAlpha thermal dilatation coefficient |
|
|
- kn elastic stifness in normal direction |
|
|
- ks elastic stifness in tangential direction |
|
|
- ft tensile strength |
|
|
- gf fracture energy |
|
|
- [maxomega] maximum damage, used for convergence improvement
(its value is between 0 and 0.999999 (default),
and it affects only the secant stiffness but not the stress) |
|
|
- [beta] parameter controlling the effect of sliding part of displacement jump on equivalent strain, default value 0 |
|
Supported modes |
2dInterface, 3dInterface |
|
Features |
|
|
Borek Patzak
2019-03-19
![]() and ks
and ks
![]() where
where ![]() is a scalar damage variable.
The damage evolution law is postulated in an explicit form, relating
the damage variable
is a scalar damage variable.
The damage evolution law is postulated in an explicit form, relating
the damage variable ![]() to the largest previously reached
equivalent “strain” level,
to the largest previously reached
equivalent “strain” level, ![]() .
.
![]() , is a scalar measure of the displacement jump vector. The choice of the specific expression
for the equivalent strain affects the shape of the elastic domain
in the strain space and plays a similar role to the choice of a yield
condition in plasticity.
Currently, in the present implementation, the equivalent strain is given by
, is a scalar measure of the displacement jump vector. The choice of the specific expression
for the equivalent strain affects the shape of the elastic domain
in the strain space and plays a similar role to the choice of a yield
condition in plasticity.
Currently, in the present implementation, the equivalent strain is given by