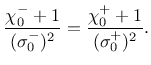| Description |
Anisotropic elastoplastic model with isotropic damage |
| Record Format |
TrabBone3d (in) #
d(rn) # eps0(rn) # nu0(rn) # mu0(rn) # expk(rn) # expl(rn) # m1(rn) # m2(rn) # rho(rn) #
sig0pos(rn) # sig0neg(rn) # chi0pos(rn) # chi0neg(rn) # tau0(rn) # plashardfactor(rn) # expplashard(rn) # expdam(rn) # critdam(rn) # |
| Parameters |
- material number |
| |
- d material density |
| |
- eps0 Young modulus (at zero porosity) |
| |
- nu0 Poisson ratio (at zero porosity) |
| |
- mu0 shear modulus of elasticity (at zero porosity) |
| |
- m1 first eigenvalue of the fabric tensor |
| |
- m2 second eigenvalue of the fabric tensor |
| |
- rho volume fraction of solid phase |
| |
- sig0pos yield stress in tension |
| |
- sig0neg yield stress in compression |
| |
- tau0 yield stress in shear |
| |
- chi0pos interaction coefficient in tension |
| |
- plashardfactor hardening parameter |
| |
- expplashard exponent in hardening law |
| |
- expdam exponent in damage law |
| |
- critdam critical damage |
| |
- expk exponent 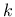 in the expression for elastic stiffness in the expression for elastic stiffness |
| |
- expl exponent 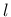 in the expression for elastic stiffness in the expression for elastic stiffness |
| |
- expq exponent 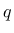 in the expression for tensor in the expression for tensor 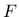 |
| |
- expp exponent 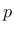 in the expression for tensor in the expression for tensor 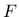 |
| Supported modes |
3dMat |
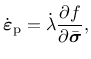
![$\displaystyle =\left[\begin{array}{cccccc}
\frac{1}{E_1} & -\frac{\nu_{12}}{E_1...
...1}{G_{13}} & 0\\
0 & 0 & 0 & 0 & 0 & \frac{1}{G_{12}}
\end{array}\right]^{-1},$](img886.png)
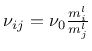 . Here,
. Here, ![]() that is used in the yield condition. The yield condition is divided into tensile and compressive parts. Tensor
that is used in the yield condition. The yield condition is divided into tensile and compressive parts. Tensor
![]() is different in each part of the effective stress space. This tensor is denoted
is different in each part of the effective stress space. This tensor is denoted
![]()
![]() in tensile part, characterized by
in tensile part, characterized by
![]() and
and
![]()
![]() in compressive part, characterized by
in compressive part, characterized by
![]() , where
, where
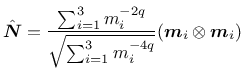
![$\displaystyle =\left[\begin{array}{cccccc}
\frac{1}{\left({\sigma_{1}^{\pm}}\ri...
...}{\tau_{13}} & 0\\
0 & 0 & 0 & 0 & 0 & \frac{1}{\tau_{12}}
\end{array}\right].$](img899.png)
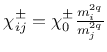 is the so-called interaction coefficient,
is the so-called interaction coefficient,