Latticedamage2d

This is a damage lattice material used together with latticedamage2d elements. It uses a scalar damage relationship of the form

$$\boldsymbol{\sigma} = \left(1-\omega\right) \mathbf{D}_{\rm e} \boldsymbol{\varepsilon}$$ (233)

where $\boldsymbol{\sigma} = \left( \sigma_{\rm n}, \sigma_{\rm t}, \sigma_{\rm\phi}\right)^{T}$ is a vector of tractions and $\boldsymbol{\varepsilon} = \left( \varepsilon_{\rm n}, \varepsilon_{\rm t}, \varepsilon_{\rm\phi}\right)^{T}$ is a vector of strains obtained from displacement jumps smeared over the element length. Furthermore, $\omega$ is the damage variable varying from 0 (undamaged) to 1 (fully damaged). Also, $\mathbf{D}_{\rm e}$ is the elastic stiffness matrix which is based on the elastic modulus of the lattice material $E$, and a parameter $\gamma$ which is the ratio of the modulus of the shear and normal direction. The strength envelope is elliptic (Figure 13) and determined by three parameters, $f_{\rm t}$, $f_{\rm q}$ and $f_{\rm c}$. The evolution of the damage variable $\omega$ is controlled by normal stress-normal crack opening law. The three possible laws are linear, bilinear and exponential (Figure 14).

Figure 13: Strength envelope of LatticeDamage2d.

Figure 14: Softening types of LatticeDamage2d: (a) linear softening, (b) bilinear softening, (c) exponential softening.

The model parameters are summarised in Tab. 51.

Table 51: Scalar damage model for 2d lattice elements - summary.

Description	Saclar damage model for lattice2d
Record Format	latticedamage2d (in) # d(rn) # talpha(rn) # e(rn) # a1(rn) # a2(rn) # e0(rn) # coh(rn) # ec(rn) # stype(rn) # wf(rn) # wf1(rn) #
Parameters	- material number
	- d material density
	- talpha Thermal exansion coefficient
	- e normal modulus of lattice material
	- a1 ratio of shear and normal modulus
	- a2 ratio of rotational and normal modulus. Optional parameter. Default is 1.
	- e0 strain at tensile strength: $f_{\rm t}/E$
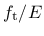	- coh ratio of shear and tensile strength: $f_{\rm q}/f_{\rm t}$
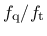	- ec ratio of compressive and tensile strength: $f_{\rm c}/f_{\rm t}$
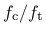	- stype softening types: 1-linear, 2-bilinear and 3-exponential
	- wf displacement threshold related to fracture energy used in all three softening types.
Supported modes	2dlattice