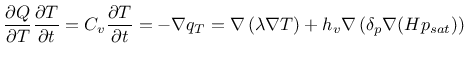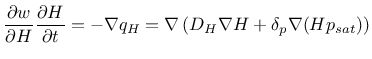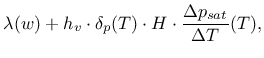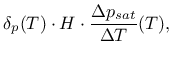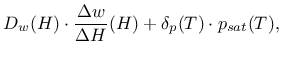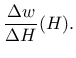next up previous contents
Next: Material for unsaturated flow Up: Material Models for Transport Previous: Coupled heat and mass

Coupled heat and mass transport material model - HeMoKunzel

The presented formulation is based on the work of Kuenzel [15]. The model is suitable for problems with dominating water diffusion and negligible water convection. The governing equations for temperature and humidity reads


$\displaystyle \frac{\partial Q}{\partial t}$ $\displaystyle =$ $\displaystyle \frac{\partial Q}{\partial T} \frac{\partial T}{\partial t} = C_v... ...mbda \nabla T \right ) + h_v \nabla \left( \delta_p \nabla (H p_{sat}) \right )$ (251)
$\displaystyle \frac{\partial w}{\partial t}$ $\displaystyle =$ $\displaystyle \frac{\partial w}{\partial H} \frac{\partial H}{\partial t} = -\nabla q_H = \nabla \left( D_H \nabla H + \delta_p \nabla (H p_{sat}) \right )$ (252)


Table 60: Parameters from Kunzel's model.
$T$ (K) Temperature
$H$ (-) Relative humidity 0-1
$\frac{\partial Q}{\partial T} \approx C_v$ J/K/m$^3$ Heat storage capacity per volume
$\frac{\partial w}{\partial H}$ kg/m$^3$ Moisture storage capacity - sorption isotherm
$Q$ J/m$^3$ Total amount of heat in unit volume
$q_T$ W/m$^2$ Heat flux
$\lambda$ W/m/K Thermal conductivity
$h_v$ J/kg Evaporation enthalpy of water
$\delta_p$ kg/m/s/Pa Water vapour permeability
$p_{sat}$ Pa Water vapour saturation pressure
$w$ kg/m$^3$ Moisture content
$D_H$ kg/m/s Liquid conduction coefficient
$D_w$ m$^2$/s Water diffusivity


Numerical solution leads to the system of equations

$\displaystyle \left[ \begin{array}{cc} \mbox{\boldmath$K$}_{TT} & \mbox{\boldma... ...y}{c} \mbox{\boldmath$q$}_{T} \\ \mbox{\boldmath$q$}_{H} \end{array} \right\},$     (253)

where
$\displaystyle \mbox{\boldmath$K$}$$\displaystyle _{TT} = \int_{\Omega}$   $\displaystyle \mbox{\boldmath$B$}$$\displaystyle ^T k_{TT}$   $\displaystyle \mbox{\boldmath$B$}$$\displaystyle {\rm d}\Omega,$   $\displaystyle \mbox{\boldmath$K$}$$\displaystyle _{TH} = \int_{\Omega}$   $\displaystyle \mbox{\boldmath$B$}$$\displaystyle ^T k_{Th}$   $\displaystyle \mbox{\boldmath$B$}$$\displaystyle {\rm d}\Omega,\qquad$     (254)


$\displaystyle \mbox{\boldmath$K$}$$\displaystyle _{HT} = \int_{\Omega}$   $\displaystyle \mbox{\boldmath$B$}$$\displaystyle ^T k_{hT}$   $\displaystyle \mbox{\boldmath$B$}$$\displaystyle {\rm d}\Omega,$   $\displaystyle \mbox{\boldmath$K$}$$\displaystyle _{HH} = \int_{\Omega}$   $\displaystyle \mbox{\boldmath$B$}$$\displaystyle ^T k_{hh}$   $\displaystyle \mbox{\boldmath$B$}$$\displaystyle {\rm d}\Omega,\qquad$     (255)


$\displaystyle \mbox{\boldmath$C$}$$\displaystyle _{TT} = \int_{\Omega}$   $\displaystyle \mbox{\boldmath$N$}$$\displaystyle ^T c_{TT}$   $\displaystyle \mbox{\boldmath$N$}$$\displaystyle {\rm d}\Omega,$   $\displaystyle \mbox{\boldmath$C$}$$\displaystyle _{TH} = \int_{\Omega}$   $\displaystyle \mbox{\boldmath$N$}$$\displaystyle ^T c_{Th}$   $\displaystyle \mbox{\boldmath$N$}$$\displaystyle {\rm d}\Omega,\qquad$     (256)


$\displaystyle \mbox{\boldmath$C$}$$\displaystyle _{HT} = \int_{\Omega}$   $\displaystyle \mbox{\boldmath$N$}$$\displaystyle ^T c_{hT}$   $\displaystyle \mbox{\boldmath$N$}$$\displaystyle {\rm d}\Omega,$   $\displaystyle \mbox{\boldmath$C$}$$\displaystyle _{HH} = \int_{\Omega}$   $\displaystyle \mbox{\boldmath$N$}$$\displaystyle ^T c_{hh}$   $\displaystyle \mbox{\boldmath$N$}$$\displaystyle {\rm d}\Omega,\qquad$     (257)


$\displaystyle \mbox{\boldmath$q$}$$\displaystyle _T = \int_{\Gamma_2}$   $\displaystyle \mbox{\boldmath$N$}$$\displaystyle ^T \overline{q}_{T}{\rm d}\Gamma,$   $\displaystyle \mbox{\boldmath$q$}$$\displaystyle _H = \int_{\Gamma_2}$   $\displaystyle \mbox{\boldmath$N$}$$\displaystyle ^T \overline{q}^{h}{\rm d}\Gamma,\qquad$     (258)

where


$\displaystyle k_{TT}$ $\displaystyle =$ $\displaystyle \lambda(w) + h_v \cdot \delta_p(T) \cdot H \cdot \frac{\Delta p_{sat}}{\Delta T}(T),$ (259)
$\displaystyle k_{TH}$ $\displaystyle =$ $\displaystyle h_v \cdot \delta_p(T) \cdot p_{sat}(T),$ (260)
$\displaystyle k_{HT}$ $\displaystyle =$ $\displaystyle \delta_p(T) \cdot H \cdot \frac{\Delta p_{sat}}{\Delta T}(T),$ (261)
$\displaystyle k_{HH}$ $\displaystyle =$ $\displaystyle D_w(H) \cdot \frac{\Delta w}{\Delta H}(H) + \delta_p(T) \cdot p_{sat}(T),$ (262)
$\displaystyle c_{TT}$ $\displaystyle =$ $\displaystyle C_s \cdot \rho + C_w \cdot w,$ (263)
$\displaystyle c_{TH}$ $\displaystyle =$ $\displaystyle 0,$ (264)
$\displaystyle c_{HT}$ $\displaystyle =$ $\displaystyle 0,$ (265)
$\displaystyle c_{HH}$ $\displaystyle =$ $\displaystyle \frac{\Delta w}{\Delta H}(H).$ (266)

Note, that conductivity matrix $K$ is unsymmetric hence unsymmetric matrix storage needs to be used (smtype).

The model parameters are summarized in Tab. 61.

Table 61: Coupled heat and mass transfer material model Kunzel - summary.
Description Coupled heat and mass transfer material model
Record Format HeMoKunzel num(in) # d(rn) # iso_type(in) # iso_wh(rn) # mu(rn) # permeability_type(in) # A(rn) # lambda0(rn) # b(rn) # cs(rn) # [ pl(rn) #] [ rhoH2O(rn) #] [ cw(rn) #] [ hv(rn) #]
Parameters -num material model number
  -d bulk density of dry building material [kg/m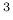$^3$]
  -iso_type=0 is isotherm from Hansen needing iso_n, iso_a, =1 is Kunzel which needs iso_b
  -iso_wh maximum adsorbed water content [kg/m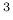$^3$]
  -mu water vapor diffusion resistance [-]
  -permeability_type =0 is Multilin_h needing perm_h, perm_Dw(h), =1 is Multilin_wV needs perm_wV, perm_DwwV, =2 is Kunzelperm needs A as water absorption coefficient [kg/m/s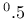$^0.5$]
  -lambda0rn thermal conductivity [W/m/K]
  -b thermal conductivity supplement [-]
  -cs specific heat capacity of the building material [J/kg/K]
  -[pl] ambient air pressure [Pa], default = 101325
  -[rhoH2O] water density [kg/m3], default = 1000
  -[cw] specific heat capacity of liquid water, default = 4183
  -[hv] latent heat of water phase change [J/kg], default = 2.5e+6
Supported modes _2dHeMo, _3dHeMo


next up previous contents
Next: Material for unsaturated flow Up: Material Models for Transport Previous: Coupled heat and mass
Borek Patzak
2019-03-19