One-dimensional transport element

The discrete form of the differential equation for mass transport for a one-dimensional transport element is

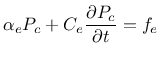$$\alpha_{e}P_{c} + C_{e}\frac{\partial P_{c}}{\partial t} = f_{e}$$ (271)

where 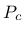$P_{c}$ is a vector containing the nodal values of the capillary pressure, 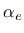$\alpha_{e}$ is the conductivity matrix, 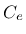$C_{e}$ is the capacity matrix and 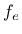$f_{e}$ is the nodal flow rate vector ($kg.m^{3}$).

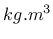The capacity matrix is

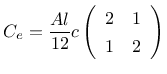$$C_{e} = \frac{Al}{12}c \left( \begin{array}{ c c } 2 & 1 \\ 1 & 2 \end{array} \right)$$ (272)

where 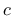$c$ is the capacity of the material, l is the length of the transport element and 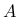$A$ is the cross-sectional area of the transport element.

The conductivity matrix is defined as

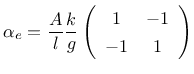$$\alpha_{e} = \frac{A}{l}\frac{k}{g} \left( \begin{array}{ c c } 1 & -1 \\ -1 & 1 \end{array} \right)$$ (273)