Bingham fluid - BinghamFluid
Constitutive model of Bingham fluid. This is a constitutive model of
non-Newtonian type. The model parameters are summarized
in Tab. 64.
In the Bingham model the flow is characterized by following
constitutive equation
where
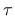 is the shear stress applied to material,
is the shear stress applied to material,
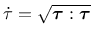 is the shear stress measure,
is the shear stress measure,
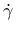 is
the shear rate,
is
the shear rate,
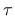
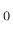 is the yield stress, and
is the yield stress, and 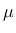 is the plastic
viscosity.
The parameters for the model can be in general determined using two
possibilities: (i) stress controlled rheometer, when the stress is applied
to material and shear rate is measured, and (ii) shear rate controlled
rheometer, where concrete is sheared and stress is measured. However,
most of the widely used tests are unsatisfactory in the sense, that
they measure only one parameter. These one-factor tests include slump
test, penetrating rod test, and Ve-Be test. Recently, some tests
providing two parameters on output have been designed (BTRHEOM, IBB,
and BML rheometers). Also a refined version of the
standard slump test has been developed for estimating yield stress and
plastic viscosity. The test is based on measuring the time necessary
for the upper surface of the concrete cone in the slump to fall a
distance 100 mm. Semi-empirical models are then proposed for estimating
yield stress and viscosity based on measured results. The advantage
is, that this test does not require any special equipment, provided that
the one for the standard version is available.
is the plastic
viscosity.
The parameters for the model can be in general determined using two
possibilities: (i) stress controlled rheometer, when the stress is applied
to material and shear rate is measured, and (ii) shear rate controlled
rheometer, where concrete is sheared and stress is measured. However,
most of the widely used tests are unsatisfactory in the sense, that
they measure only one parameter. These one-factor tests include slump
test, penetrating rod test, and Ve-Be test. Recently, some tests
providing two parameters on output have been designed (BTRHEOM, IBB,
and BML rheometers). Also a refined version of the
standard slump test has been developed for estimating yield stress and
plastic viscosity. The test is based on measuring the time necessary
for the upper surface of the concrete cone in the slump to fall a
distance 100 mm. Semi-empirical models are then proposed for estimating
yield stress and viscosity based on measured results. The advantage
is, that this test does not require any special equipment, provided that
the one for the standard version is available.
In order to avoid numerical difficulties caused by the existence of
the sharp angle in material model
response at
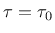 , the numerical implementation uses
following smoothed relation for viscosity
, the numerical implementation uses
following smoothed relation for viscosity
where 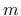 is so called stress growth parameter. The higher value of
parameter
is so called stress growth parameter. The higher value of
parameter 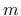 , the closer approximation of the original
constitutive equation (278) is obtained.
, the closer approximation of the original
constitutive equation (278) is obtained.
Table 64:
Bingham Fluid material - summary.
| Description |
Bingham fluid material |
| Record Format |
BinghamFluid num(in) #
d(rn) # mu0(rn) # tau0(rn) # |
| Parameters |
- num material model number |
| |
- d material density |
| |
- mu0 viscosity |
| |
- tau0 Yield stress |
| Supported modes |
2d, 3d flow |
|
Borek Patzak
2019-03-19
![]() , the numerical implementation uses
following smoothed relation for viscosity
, the numerical implementation uses
following smoothed relation for viscosity