Export modules

Export modules allow to export computed data into external software for post-processing. The number of export module records is specified in analysis record using nmodules parameter (see the initial part of section 3). The general format is the following:

*EntType	[tstep_all]
	[tstep_step #(in)]
	[tsteps_out #(rl)]
	[subtsteps_out #(in)]
	[domain_all]
	[domain_mask #(in)]

To select all solution steps, in which output will be performed, use tstep_all. To select each tstep_step-nth step, use tstep_step parameter. In order to select only specific solution steps, the tsteps_out list can be specified, supplying solution step number list in which output will be done. To select output for all domain of the problem the domain_all keyword can be used. To select only specific domains, domain_mask array can be used, where the values of the array specify the domain numbers to be exported. If the parameter subtsteps_out = 1, it turns on the export of intermediate results, for example during the substepping or individual equilibrium iterations. This option requires support from the solver.

Currently, the supported export modules are following

• VTK export, DEPRECATED - Use VTKXML

  vtk	[vars #(ia)]
  	[primvars #(ia)]
  	[cellvars #(ia)]
  	[stype #(in)]
  	[regionstoskip #(ia)]

  
  

  vtkxml	[vars #(ia)]
  	[primvars #(ia)]
  	[cellvars #(ia)]
  	[ipvars #(ia)]
  	[stype #(in)]
  	[regionsets #(ia)]
  	[timeScale #(rn)]

  
  

  • The vtk module is obsolete, use vtkxml instead. Vtkxml allows to export results recovered on region by region basis and has more features.

  • The array vars contains identifiers for those internal variables which are to be exported. These variables will be smoothed and transfered to nodes. The id values are defined by InternalStateType enumeration, which is defined in include file ``src/oofemlib/internalstatetype.h''.

  • The array primvars contains identifiers of primary variables to be exported. The possible values correspond to the values of enumerated type UnknownType, which is again defined in ``src/oofemlib/unknowntype.h''. Please note, that the values corresponding to enumerated type values start from zero, if not specified directly and that not all values are supported by particular material model or analysis type.

  • The array cellvars contains identifiers of constant variables defined on an element (cell), e.g. a material number. Identifier numbers are specified in ``src/oofemlib/internalstatetype.h''.

  • The array ipvars contains identifiers for those internal variables which are to be exported. These variables will be directly exported (no smoothing) as point dataset, where each point corresponds to individual integration point. A separate vtu file for these raw, point data will be created. The id values are defined by InternalStateType enumeration, which is defined in include file ``src/oofemlib/internalstatetype.h''.

  • The parameter stype allows to select smoothing procedure for internal variables, which is used to compute nodal values from values in integration points. The supported values are 0 for simple nodal averageing (generally supported only by triangular and tetrahedral elements), 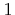$1$ for Zienkiewicz Zhu recovery (default), and 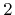$2$ for Superconvergent Patch Recovery (SPR, based on least square fitting).

  • The export is done on region basis, on each region, the nodal recovery is performed independently and results are exported in a separate piece. This allows to take into account for discntinuities, or to export variables defined only by particular material model. The region volumes are defined using sets containing individual elements. By default the one region is created, containing all element in the problem domain. The optional parameter regionsets allows to use user-defined. The individual values refer to numbers (ids) of domain sets. Note, that regions are determined solely using elements.

    vtkxml tstep_all cellvars 1 46 vars 1 1 primvars 1 1 stype 2 regionsets 2 1 2

  • timeScale scales time in output. In transport problem, basic units are seconds. Setting timeScale = 2.777777e-4 (=1/3600.) converts all time data in vtkXML from seconds to hours.

  By default vtk and vtkxml modules perform recovery over the whole domain. The VTKXML module can operate in region-by-region mode (see nvr and vrmap parameters). In this case, the smoothing is performed only over particular virtual region, where only elements in this virtual region participate.

• Homogenization of IP quantities in the global coordinate system (such as stress, strain, damage, heat flow). Corresponding IP quantities are summed and averaged over the volume. It is possible to select region sets from which the averaging occurs. The averaging works for all domains with an extension to trusses. A truss is considered as a volume element with oriented stress and strain components along the truss axis. The transformation to global components occurs before averaging.

  	ists #(ia)
  	[scale #(rn)]
  	[regionSets #(ia)]

  
  

  • An integer array ists specifies internal state types for export which are defined in internalstatetype.h file.

  • The parameter scale multiplies all averaged IP quantities. scale=1 by default.

  • An integer array regionSets specifies region sets for averaging. All domain is averaged by default.

• Gauss point export is useful if one needs to plot a certain variable (such as damage) as a function of a spatial coordinate using tools like gnuplot. It generates files with data organized in columns, each row representing one Gauss point. In this way, one can plot e.g. the damage distribution along a one-dimensional bar.

  gpexportmodule	[vars #(ia)]
  	[ncoords #(in)]

  
  

  • The array vars contains identifiers for those internal variables which are to be exported. The id values are defined by InternalStateType enumeration, which is defined in include file ``src/oofemlib/internalstatetype.h''.
  • Parameter ncoords specifies the number of spatial coordinates to be exported at each Gauss point. Depending on the spatial dimension of the domain, the points can have one, two or three coordinates. If ncoords is set to -1, only those coordinates that are actually used are exported. If ncoords is set to 0, no coordinates are exported. If ncoords is set to a positive integer, exactly ncoords coordinates are exported. If ncoords exceeds the actual number of coordinates, the actual coordinates are supplemented by zeros. For instance, if we deal with a 2D problem, the actual number of coordinates is 2. For ncoords=3, the two actual coordinates followed by 0 will be exported. For ncoords=1, only the first coordinate will be exported.
  The Gauss point export module creates a file with extension ``gp'' after each step for which the output is performed. This file contains a header with lines starting by the symbol #, followed by the actual data section. Each data line corresponds to one Gauss point and contains the following data:
  1. element number,
  2. material number,
  3. Gauss point number,
  4. contributing volume around Gauss point,
  5. Gauss point global coordinates (written as a real array of length ncoords),
  6. internal variables according to the specification in vars (each written as a real array of the corresponding length).
  Example:
  ``GPExportModule 1 tstep_step 100 domain_all ncoords 2 vars 5 4 13 31 64 65''
  means that the *.gp file will be written after each 100 steps and will contain for each of the Gauss points in the entire domain its 2 coordinates and also internal variables of type 4, 13, 31, 64 and 65, which are the strain tensor, damage tensor, maximum equivalent strain level, stress work density and dissipated work density. Of course, the material model must be able to deliver such variables. The size of the strain tensor depends on the spatial dimension, and the size of the damage tensor depends on the spatial dimension and type of model (e.g., for a simple isotropic damage model it will have just 1 component while for an anisotropic damage model it may have more). The other variables in this example are scalars, but they will be written as arrays of length 1, so the actual value will always be preceded by ``1'' as the length of the array. Since certain internal variables have the meaning of densities (per unit volume or area, again depending on the spatial dimension), it is useful to have access to the contributing volume of the Gauss point. The product of this contributing volume and the density gives an additive contribution to the total value of the corresponding variable. This can be exploited e.g. to evaluate the total dissipated energy over the entire domain.