Geometric nonlinear analysis

2.14 Geometric nonlinear analysis

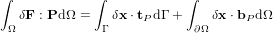
To take int account geometric nonlinearity for a specific element, the keyword nlgeo must be specified. The nlgeo parameter defines which formulation of the momentum balance is solved and what deformation measure that is computed and sent to the consitiutive models (see Table 49). If nlgeo=1, then the momentum balance is set up in the reference configuration in terms of the First Piola-Kirchhoff stress tensor P and the deformation tensor F as energy conjugates. This is also refered to a Total Lagrangian formulation. The balance equation in weak form reads

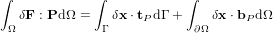∫ ∫ ∫ δF : Pd Ω = δx⋅t dΓ + δx⋅b dΩ Ω Γ P ∂Ω P

(6)

This equation can be rewritten in terms of the displacement u and the displacement gradient H

∫ ∫ ∫ δH : Pd Ω = δu ⋅tP dΓ + δu⋅bP dΩ Ω Γ ∂Ω

(7)

This equation is nearly identical to the one for small strains except that another stress measure is used and we have the virtual displacement gradient instead of the virtual strains.

The corresponding FE-formulation is obtained as

∫ ∫ ∫ BTH ⋅Pd Ω = NT ⋅tPdΓ + δNT ⋅bPdΩ Ω Γ ∂Ω

(8)

with the tangent stiffness

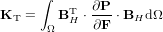∫ ∂P KT = BTH ⋅---⋅BHd Ω Ω ∂F

(9)

Thus, for an element to support large deformations (in addition to small deformation) it needs only to implement the B_H matrix. Similar to the regular B matrix, which gives the strains in Voigt form when multiplied with the solution vector a, B_H should give the displcement gradient in Voigt form with 9 components for a full 3D state.


nlgeo	strain tensor

0 (default)	Small-strain tensor
1	Green-Lagrange strain tensor
2	Deformation gradient

Table 49: Nonlinear geometry modes

[next] [prev] [prev-tail] [front] [up]