3d Continuum Elements

2.8 3d Continuum Elements

2.8.1 LSpace element

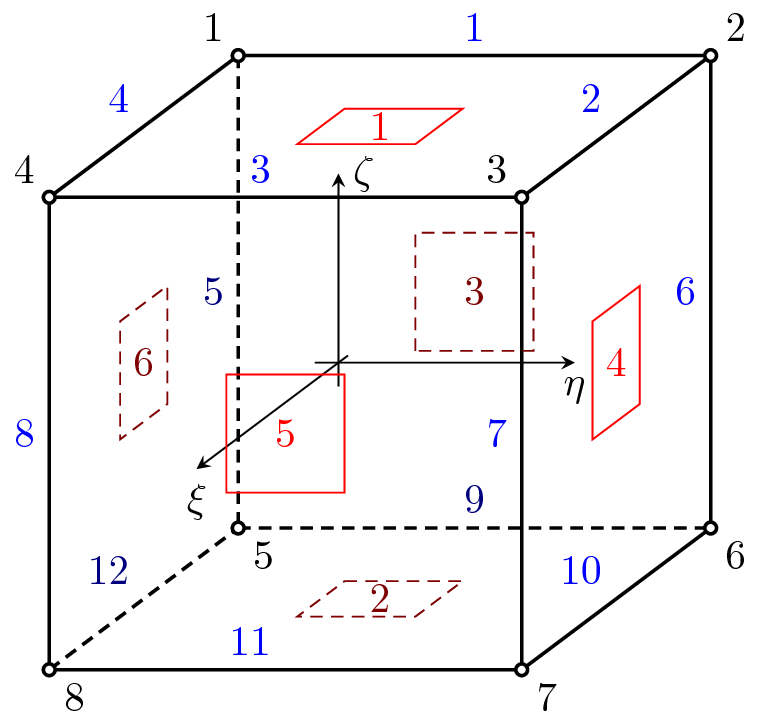
Implementation of Linear 3d eight - node finite element. Each node has 3 degrees of freedom. The element features are summarized in Table 33.

Figure 12: LSpace element (Node numbers in black, side numbers in blue, and surface numbers in red).


Keyword	lspace
Description	Linear isoparametric brick element
Specific parameters	[NIP #(in)]

Parameters	NIP: allows to set the number of integration points (possible completions are 1, 8 (default), or 27).
Unknowns	Three dofs (u-displacement, v-displacement, w-displacement) are required in each node.
Approximation	Linear approximation of displacement and geometry.
Integration	Full integration of all strain components.
Features	Adaptivity support, Geometric nonlinearity support.
CS properties	-
Loads	-
Nlgeo	0,1,2.
Status	Reliable

Table 33: lspace element summary

2.8.2 LSpaceBB element

Implementation of 3d brick eight - node linear approximation element with selective integration of deviatoric and volumetric strain contributions (B-bar formulation) for incompressible problems. Features and description identical to conventional lspace element, see section 2.8.1.

2.8.3 QSpace element

Implementation of quadratic 3d 20-node finite element. Each node has 3 degrees of freedom. The element features are summarized in Table 34.

Figure 13: QSpace element.


Keyword	qspace
Description	Quadratic isoparametric brick element
Specific parameters	[NIP #(in)]

Parameters	NIP: allows to set the number of integration points (possible completions are 1, 8 (default), or 27).
Unknowns	Three dofs (u-displacement, v-displacement, w-displacement) are required in each node.
Approximation	Quadratic approximation of displacement and geometry.
Integration	Full integration of all strain components.
Features	-
CS properties	-
Loads	-
Nlgeo	0,1,2.
Status	Reliable

Table 34: qspace element summary

2.8.4 LTRSpace element

Implementation of tetrahedra four-node finite element. Each node has 3 degrees of freedom. The element features are summarized in Table 35. Following node numbering convention is adopted (see also Fig. 14):

Select a face that will contain the first three corners. The excluded corner will be the last one.
Number these three corners in a counterclockwise sense when looking at the face from the excluded corner.

Figure 14: LTRSpace element. Definition and node numbering convention.


Keyword	LTRSpace
Description	Linear tetrahedra element
Specific parameters	-

Unknowns	Three dofs (u-displacement, v-displacement, w-displacement) are required in each node.
Approximation	Linear approximation of displacements and geometry using linear volume coordinates.
Integration	Full integration of all strain components using four point Gauss integration formula.
Features	Adaptivity support, Geometric nonlinearity support.
CS properties	-
Loads	Surface and Edge loadings supported.
Nlgeo	0,1,2.
Status	Reliable

Table 35: LTRSpace element summary

2.8.5 QTRSpace element

Implementation of tetrahedra ten-node finite element. Each node has 3 degrees of freedom. The element features are summarized in Table 36. Following node numbering convention is adopted (see also Fig. 15):

Figure 15: QTRSpace element. Definition and node numbering convention.


Keyword	QTRSpace
Description	3D tetrahedra element with quadratic interpolation
Specific parameters	[NIP #(in)]

Parameters	NIP: allows to alter the default integration formula (possible completions are 1, 4 (default), 5, 11, 15, 24, and 45 point intergartion formulas).
Unknowns	Three dofs (u-displacement, v-displacement, w-displacement) are required in each node.
Approximation	Quadratic approximation of displacements and geometry using linear volume coordinates.
Integration	Full integration of all strain components using four point Gauss integration formula.
Features	-
CS properties	-
Loads	-
Nlgeo	0,1,2.
Status	Reliable

Table 36: QTRSpace element summary

2.8.6 LWedge element

Implementation of wedge six-node finite element. Each node has 3 degrees of freedom. The element features are summarized in Table 37. Following node numbering convention is adopted (see also Fig. 16):

Figure 16: LWedge element. Node numbering convention in black, edge numbering in blue and face numbering in red.


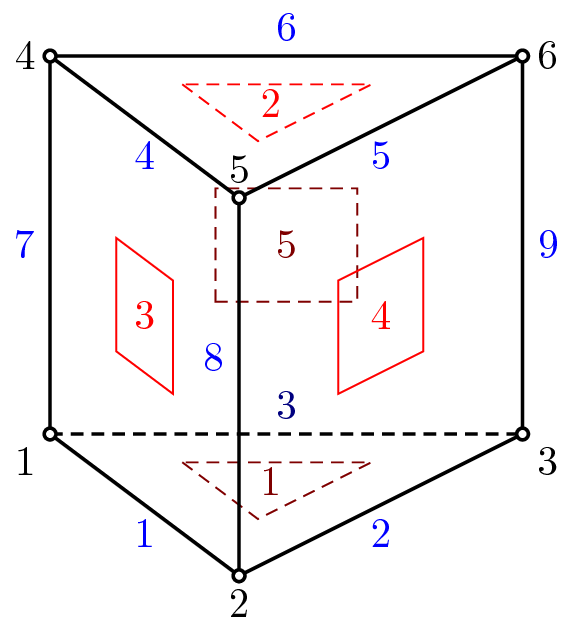
Keyword	LWedge
Description	3D wedge six-node finite element with linear interpolation
Specific parameters	[NIP #(in)]

Parameters	NIP: allows to alter the default integration formula (possible completions are 2 (default) and 9 point integration formulas).
Unknowns	Three dofs (u-displacement, v-displacement, w-displacement) are required in each node.
Approximation	Linear approximation of displacements and geometry.
Integration	Full integration of all strain components using four point Gauss integration formula.
Features	-
CS properties	-
Loads	-
Nlgeo	0,1,2.
Status	Reliable

Table 37: LWedge element summary

2.8.7 QWedge element

Implementation of wedge fifteen-node finite element. Each node has 3 degrees of freedom. The element features are summarized in Table 38. Following node numbering convention is adopted (see also Fig. 17):

Figure 17: QWedge element. Node numbering convention in black, edge numbering in blue and face numbering in red.


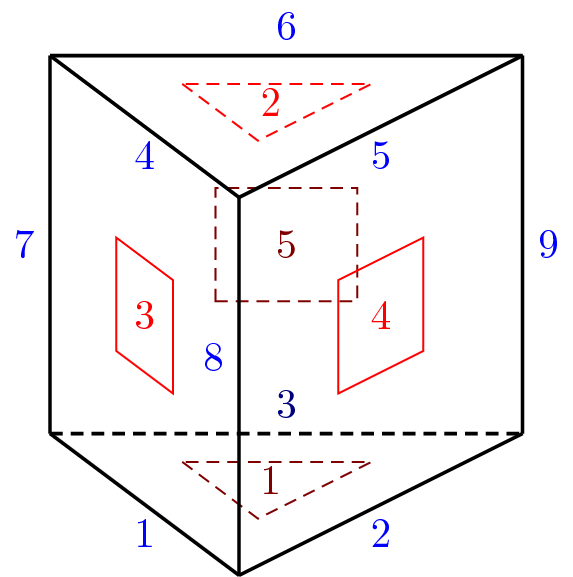
Keyword	QWedge
Description	3D wedge six-node finite element with quadratic interpolation
Specific parameters	[NIP #(in)]

Parameters	NIP: allows to alter the default integration formula (possible completions are 2 (default) and 9 point integration formulas).
Unknowns	Three dofs (u-displacement, v-displacement, w-displacement) are required in each node.
Approximation	Quadratic approximation of displacements and geometry.
Integration	Full integration of all strain components using four point Gauss integration formula.
Features	-
CS properties	-
Loads	-
Nlgeo	0,1,2.
Status	Reliable

Table 38: QWedge element summary

[next] [prev] [prev-tail] [front] [up]