Drucker-Prager model - DruckerPrager
The Drucker-Prager plasticity model1 is an isotropic elasto-plastic model based
on a yield function
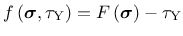 |
(19) |
with the pressure-dependent equivalent stress
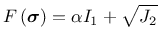 |
(20) |
As usual,
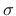 is the stress tensor,
is the stress tensor,
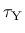 is the yield stress
under pure shear, and
is the yield stress
under pure shear, and 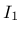 and
and 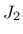 are the first invariant and second
deviatoric invariant of the stress tensor.
The friction coefficient
are the first invariant and second
deviatoric invariant of the stress tensor.
The friction coefficient 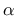 is a positive parameter that
controls the influence of the pressure on the yield limit, important for
cohesive-frictional materials such as concrete, soils or other
geomaterials. Regarding Mohr-Coulomb plasticity, relation to cohesion,
is a positive parameter that
controls the influence of the pressure on the yield limit, important for
cohesive-frictional materials such as concrete, soils or other
geomaterials. Regarding Mohr-Coulomb plasticity, relation to cohesion, 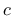 , and
the angle of friction,
, and
the angle of friction, 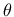 , exists for the Drucker-Prager model
, exists for the Drucker-Prager model
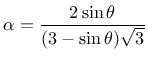 |
|
|
(21) |
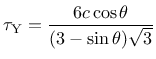 |
|
|
(22) |
The flow rule is derived from the plastic potential
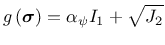 |
(23) |
where
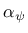 is the dilatancy coefficient. An associated
model with
is the dilatancy coefficient. An associated
model with
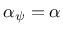 would overestimate the dilatancy of
concrete, so the dilatancy coefficient is usually chosen smaller than the
friction coefficient.
The model is described by the equations
would overestimate the dilatancy of
concrete, so the dilatancy coefficient is usually chosen smaller than the
friction coefficient.
The model is described by the equations
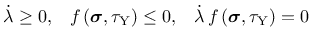 |
(28) |
which represent the linear elastic law, hardening law, evolution laws
for plastic strain and hardening variable, and the
loading-unloading conditions.
In the above,
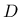 is the elastic stiffness
tensor,
is the elastic stiffness
tensor,
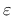 is the strain tensor,
is the strain tensor,
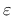
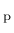 is the plastic strain tensor,
is the plastic strain tensor,
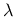 is the plastic multiplier,
is the plastic multiplier,
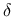 is the unit
second-order tensor,
is the unit
second-order tensor,
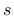 is the
deviatoric stress tensor,
is the
deviatoric stress tensor, 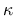 is the hardening variable, and a
superior dot marks the derivative with respect to time.
The flow rule has the form given in Eq. (26) at all
points of the conical yield surface with the exception of its vertex,
located on the hydrostatic axis.
is the hardening variable, and a
superior dot marks the derivative with respect to time.
The flow rule has the form given in Eq. (26) at all
points of the conical yield surface with the exception of its vertex,
located on the hydrostatic axis.
For the present model, the evolution
of the hardening variable can be explicitly linked to the plastic
multiplier.
Substituting the flow rule
(26) into Eq. (27) and computing the norm
leads to
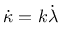 |
(29) |
with a constant parameter
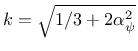 , so the
hardening variable is proportional to the plastic multiplier.
For
, so the
hardening variable is proportional to the plastic multiplier.
For
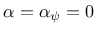 , the associated
, the associated 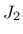 -plasticity model
is recovered as a special case.
-plasticity model
is recovered as a special case.
In the simplest case of linear hardening, the hardening function is a
linear function of 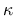 , given by
, given by
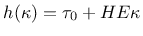 |
(30) |
where 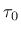 is the initial yield stress, and
is the initial yield stress, and 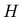 is the
hardening modulus normalized with the elastic modulus.
Alternatively, an exponential hardening function
is the
hardening modulus normalized with the elastic modulus.
Alternatively, an exponential hardening function
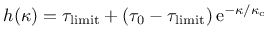 |
(31) |
can be used for a more realistic description of hardening.
The stress-return algorithm is based on the Newton-iteration.
In plasticity, this is commonly called Closest-Point-Projection (CPP),
and it generally leads to quadratic convergence.
The implemented algorithm is convergent in any stress case, but
in the vicinity of the vertex region, quadratic convergence might be
lost because of insufficient regularity of the yield function.
The algorithmic tangent stiffness matrix is implemented for both the
regular case and the vertex region.
Generally, the error decreases quadratically (of course only asymptotically).
Again, in the vicinity of the vertex region, quadratic convergence
might be lost due to insufficient regularity.
Furthermore, the tangent stiffness matrix does not always exist for
the vertex case. In these cases, the elastic stiffness is used
instead.
It is generally safer (but slower) to use the elastic stiffness if you
encounter any convergence problems, especially if your problem is
tension-dominated.
Table 8:
DP material - summary.
| Description |
DP material |
| Record Format |
DruckerPrager num(in) #
d(rn) # tAlpha(rn) # E(rn) # n(rn) #
alpha(rn) # alphaPsi(rn) # ht(in) #
iys(rn) # lys(rn) # hm(rn) # kc(rn) # [ yieldtol(rn) #] |
| Parameters |
- num material model number |
| |
- d material density |
| |
- tAlpha thermal dilatation coefficient |
| |
- E Young modulus |
| |
- n Poisson ratio |
| |
- alpha friction coefficient |
| |
- alphaPsi dilatancy coefficient |
| |
- ht hardening type, 1: linear hardening, 2: exponential
hardening |
| |
- iys initial yield stress in shear, 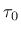 |
| |
- lys limit yield stress for exponential hardening,
 |
| |
- hm hardening modulus normalized with E-modulus (!) |
| |
- kc 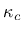 for the exponential softening law for the exponential softening law |
| |
- yieldtol tolerance of the error in the yield criterion, default value
1.e-14 |
| |
- newtonIter maximum number of iterations in 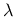 search, default value 30 search, default value 30 |
| Supported modes |
3dMat, PlaneStrain, 3dRotContinuum |
|
Borek Patzak
2019-03-19
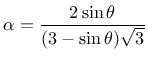
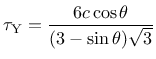
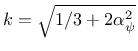 , so the
hardening variable is proportional to the plastic multiplier.
For
, so the
hardening variable is proportional to the plastic multiplier.
For
![]() , given by
, given by