| Description |
Drucker Prager material with tension cut-off |
| Record Format |
DruckerPragerCut num(in) #
d(rn) # tAlpha(rn) # E(rn) # n(rn) # tau0(rn) # alpha(rn) # [alphaPsi(rn) #] [H(rn) #] [omega_crit(rn) #] [a(rn) #] [yieldtol(rn) #] [NewtonIter(in) #] |
| Parameters |
- num material model number |
| |
- d material density |
| |
- tAlpha thermal dilatation coefficient |
| |
- E Young modulus |
| |
- n Poisson ratio |
| |
- tau0 initial yield stress in shear 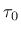 |
| |
- alpha friction coefficient |
| |
- alphaPsi dilatancy coefficient, equals to alpha by default |
| |
- H hardening modulus (can be negative in the case of plastic softening), 0 by default |
| |
- omega_crit critical damage in damage law (37), 0 by default |
| |
- a exponent in damage law (37), 0 by default |
| |
- yieldtol tolerance of the error in the yield criterion, default value
1.e-14 |
| |
- newtonIter maximum number of iterations in 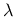 search, default value 30 search, default value 30 |
| Supported modes |
1dMat, 3dMat, PlaneStrain |
![]() controls flow associativeness; if
controls flow associativeness; if
![]() , an associate model is recovered, which
overestimates the dilatancy of concrete. Hence, the dilatancy coefficient is usually chosen smaller,
, an associate model is recovered, which
overestimates the dilatancy of concrete. Hence, the dilatancy coefficient is usually chosen smaller,
![]() , and the non-associated model is formulated.
, and the non-associated model is formulated.