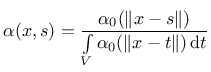Integral nonlocal formulation

One possible regularization technique is based on the integral definition of nonlocal cumulated plastic strain

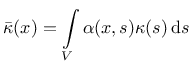$\displaystyle \bar{\kappa}(x) = \int\limits_V \alpha(x,s)\kappa(s)\,{\rm d}s$

(48)

The nonlocal weight function is usually defined as

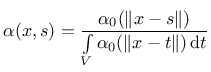$\displaystyle \alpha(x,s) = \frac{\alpha_0(\Vert x-s\Vert )}{\int\limits_V\alpha_0(\Vert x-t\Vert )\,{\rm d}t}$

(49)

where

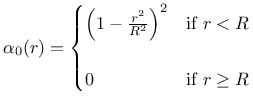$\displaystyle \alpha_0(r) = \begin{cases}\left(1-\frac{r^2}{R^2}\right)^2 &\text{if $r<R$}\\ \\ 0 & \text{if $r \ge R$} \end{cases}$

(50)

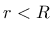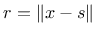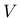is a nonnegative function, for monotonically decreasing with increasing distance $r=\Vert x-s\Vert$ , and denotes the domain occupied by the investigated material body. The key idea is that the damage evolution at a certain point depends not only on the cumulated plastic strain at that point, but also on points at distances smaller than the interaction radius 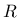, considered as a new material parameter.

Borek Patzak
2019-03-19