| Description |
Nonlocal Mises plasticity with isotropic hardening |
| Record Format |
MisesMatNl (in) # d(rn) # E(rn) # n(rn) #
sig0(rn) # H(rn) # omega_crit(rn) #a(rn) #r(rn) #m(rn) #[wft(in) #][scalingType(in) #] |
| Parameters |
- material number |
| |
- d material density |
| |
- E Young's modulus |
| |
- n Poisson's ratio |
| |
- sig0 initial yield stress in uniaxial tension (compression) |
| |
- H hardening modulus |
| |
- omega_crit critical damage |
| |
- a exponent in damage law |
| |
- r nonlocal interaction radius 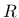 from eq. (50) from eq. (50) |
| |
- m over-nonlocal parameter |
| |
- wft selects the type of nonlocal weight function (see Section 1.5.7):
| 1 - | default, quartic spline (bell-shaped function with bounded support) |
| 2 - | Gaussian function |
| 3 - | exponential function (Green function in 1D) |
| 4 - | uniform averaging up to distance 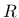 |
| 5 - | uniform averaging over one finite element |
| 6 - | special function obtained by reducing the 2D exponential function to 1D (by numerical integration)
| |
| |
- scalingType selects the type of scaling of the weight function (e.g. near a boundary; see Section 1.5.7):
| 1 - | default, standard scaling with integral of weight function in the denominator |
| 2 - | no scaling (the weight function normalized in an infinite body is used even near a boundary) |
| 3 - | Borino scaling (local complement)
| |
| Supported modes |
1dMat, PlaneStrain, 3dMat |
![]() for the integral version (and thus has the dimension
of length) but for the gradient version it has the meaning of the coefficient
for the integral version (and thus has the dimension
of length) but for the gradient version it has the meaning of the coefficient ![]() multiplying the Laplacean in (51), and thus has the dimension of length squared.
multiplying the Laplacean in (51), and thus has the dimension of length squared.