Rankine plasticity model with isotropic damage and its nonlocal formulations - RankMat, RankMatNl, RankMatGrad
This model has a very similar structure to the model described in Section 1.4.3,
but is based on the Rankine yield condition. It is available in the small-strain version
only, and so far exclusively for plane stress analysis.
The basic equations (38)-(39)
and (41)-(45) remain valid,
and the yield function (40) is redefined as
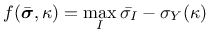 |
(53) |
where
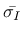 are the principal values of the effective stress tensor
are the principal values of the effective stress tensor
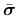 .
The hardening law can have either the linear form (42), or the exponential form
.
The hardening law can have either the linear form (42), or the exponential form
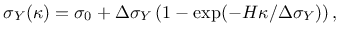 |
(54) |
where 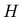 is now the initial plastic modulus and
is now the initial plastic modulus and
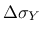 is the value of yield stress
increment asymptotically approached as
is the value of yield stress
increment asymptotically approached as
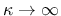 .
In damage law (45), parameter
.
In damage law (45), parameter 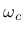 is always set to 1.
If the plastic hardening is linear, the user can specify either the exponent
is always set to 1.
If the plastic hardening is linear, the user can specify either the exponent 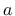 from (45),
or the dissipation per unit volume,
from (45),
or the dissipation per unit volume, 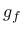 , which represents the area under the
stress-strain diagram (and parameter
, which represents the area under the
stress-strain diagram (and parameter 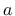 is then determined automatically such that
the area under the diagram has the prescribed value).
For exponential plastic hardening, the evaluation of
is then determined automatically such that
the area under the diagram has the prescribed value).
For exponential plastic hardening, the evaluation of 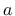 from
from 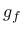 is not properly
implemented and it is better to specify
is not properly
implemented and it is better to specify 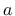 directly.
directly.
The model description and parameters are summarized in Tabs. 13-15. Note that the default value of parameter 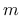 is equal to 1 for the
integral model but for the gradient model it is equal to 2.
Also note that the internal length parameter r has the meaning of the
radius of interaction
is equal to 1 for the
integral model but for the gradient model it is equal to 2.
Also note that the internal length parameter r has the meaning of the
radius of interaction 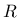 for the integral version (and thus has the dimension
of length) but for the gradient version it has the meaning of the coefficient
for the integral version (and thus has the dimension
of length) but for the gradient version it has the meaning of the coefficient 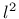 multiplying the Laplacean in (51), and thus has the dimension of length squared.
multiplying the Laplacean in (51), and thus has the dimension of length squared.
For the gradient model
it is possible to specify parameter negligible_damage, which sets the minimum
value of damage that is considered as nonzero.
The approximate solution of Helmholtz equation (51) can lead
to very small but nonzero nonlocal kappa at some points that
are actually elastic. If such small values are positive,
they lead to a very small but nonzero damage. If this is
interpreted as "loading", the tangent terms are activated,
but damage will not actually grow at such points and the
convergence rate is slowed down. It is better to consider
such points as elastic. By default, negligible_damage is set to 0,
but it is recommended to set it e.g. to 1.e-6.
Table 13:
Rankine plasticity - summary.
| Description |
Rankine plasticity with isotropic hardening and damage |
| Record Format |
RankMat (in) #
d(rn) # E(rn) # n(rn) # plasthardtype(in) # sig0(rn) # H(rn) # delSigY(rn) # yieldtol(rn) # (gf(rn) # 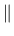 a(rn) #) a(rn) #) |
| Parameters |
- material number |
| |
- d material density |
| |
- E Young's modulus |
| |
- n Poisson's ratio |
| |
- plasthardtype type of plastic hardening (0=linear=default, 1=exponential) |
| |
- sig0 initial yield stress in uniaxial tension (compression) |
| |
- H initial hardening modulus (default value 0.) |
| |
- delSigY final increment of yield stress (default value 0., needed only if plasthardtype=1) |
| |
- yieldtol relative tolerance in the yield condition |
| |
- gf dissipation per unit volume |
| |
- a exponent in damage law (45) |
| Supported modes |
PlaneStress |
|
Table 14:
Nonlocal integral Rankine plasticity - summary.
| Description |
Nonlocal Rankine plasticity with isotropic hardening and damage |
| Record Format |
RankMatNl (in) #
d(rn) # E(rn) # n(rn) # plasthardtype(in) # sig0(rn) # H(rn) # delSigY(rn) # yieldtol(rn) # (gf(rn) # 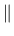 a(rn) #)r(rn) #m(rn) #[wft(in) #][scalingType(in) #] a(rn) #)r(rn) #m(rn) #[wft(in) #][scalingType(in) #] |
| Parameters |
- material number |
| |
- d material density |
| |
- E Young's modulus |
| |
- n Poisson's ratio |
| |
- plasthardtype type of plastic hardening (0=linear=default, 1=exponential) |
| |
- sig0 initial yield stress in uniaxial tension (compression) |
| |
- H initial hardening modulus (default value 0.) |
| |
- delSigY final increment of yield stress (default value 0.) |
| |
- yieldtol relative tolerance in the yield condition |
| |
- gf dissipation per unit volume |
| |
- a exponent in damage law (45) |
| |
- r internal length scale parameter 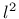 from eq. (51) from eq. (51) |
| |
- m over-nonlocal parameter (default value 1.) |
| |
- wft selects the type of nonlocal weight function (see Section 1.5.7):
| 1 - | default, quartic spline (bell-shaped function with bounded support) |
| 2 - | Gaussian function |
| 3 - | exponential function (Green function in 1D) |
| 4 - | uniform averaging up to distance 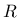 |
| 5 - | uniform averaging over one finite element |
| 6 - | special function obtained by reducing the 2D exponential function to 1D (by numerical integration)
| |
| |
- scalingType selects the type of scaling of the weight function (e.g. near a boundary; see Section 1.5.7):
| 1 - | default, standard scaling with integral of weight function in the denominator |
| 2 - | no scaling (the weight function normalized in an infinite body is used even near a boundary) |
| 3 - | Borino scaling (local complement)
| |
| Supported modes |
PlaneStress |
|
Table 15:
Gradient-enhanced Rankine plasticity - summary.
| Description |
Gradient-enhanced Rankine plasticity with isotropic hardening and damage |
| Record Format |
RankMatGrad (in) #
d(rn) # E(rn) # n(rn) # plasthardtype(in) # sig0(rn) # H(rn) # delSigY(rn) # yieldtol(rn) # (gf(rn) # 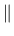 a(rn) #)r(rn) #m(rn) #negligible_damage(rn) # a(rn) #)r(rn) #m(rn) #negligible_damage(rn) # |
| Parameters |
- material number |
| |
- d material density |
| |
- E Young's modulus |
| |
- n Poisson's ratio |
| |
- plasthardtype type of plastic hardening (0=linear=default, 1=exponential) |
| |
- sig0 initial yield stress in uniaxial tension (compression) |
| |
- H hardening modulus (default value 0.) |
| |
- delSigY final increment of yield stress (default value 0.) |
| |
- yieldtol relative tolerance in the yield condition |
| |
- gf dissipation per unit volume |
| |
- a exponent in damage law (45) |
| |
- r internal length scale parameter 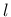 from eq. (51) from eq. (51) |
| |
- m over-nonlocal parameter (default value 2.) |
| |
- negligible_damage optional parameter (default value 0.) |
| Supported modes |
PlaneStress |
|
Borek Patzak
2019-03-19
![]() is equal to 1 for the
integral model but for the gradient model it is equal to 2.
Also note that the internal length parameter r has the meaning of the
radius of interaction
is equal to 1 for the
integral model but for the gradient model it is equal to 2.
Also note that the internal length parameter r has the meaning of the
radius of interaction ![]() for the integral version (and thus has the dimension
of length) but for the gradient version it has the meaning of the coefficient
for the integral version (and thus has the dimension
of length) but for the gradient version it has the meaning of the coefficient ![]() multiplying the Laplacean in (51), and thus has the dimension of length squared.
multiplying the Laplacean in (51), and thus has the dimension of length squared.