Next: Input Record Up: Anisotropic damage model - Previous: Local formulation
Nonlocal formulation of the MDM model is based on the averaging of
the inverse integrity tensor. This roughly corresponds to the nonlocal
isotropic damage model with averaging of the compliance variable
![]() , which does not cause any spurious locking effects.
In equation (81) for the evaluation of the damage effect tensor,
the inverse integrity tensor is replaced by its weighted average with
components
, which does not cause any spurious locking effects.
In equation (81) for the evaluation of the damage effect tensor,
the inverse integrity tensor is replaced by its weighted average with
components
By fitting a wide range of numerical results, it has been found that
the parameters of the nonlocal MDM model can be estimated from the
measurable material properties using the formulas
| (88) | |||
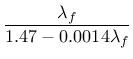 |
(89) | ||
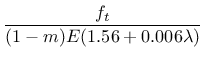 |
(90) | ||
| (91) |