Mazars damage model for concrete - MazarsModel

This isotropic damage model assumes that the stiffness degradation is isotropic, i.e., stiffness moduli corresponding to different directions decrease proportionally and independently of direction of loading. It introduces two damage parameters $\omega_t$ and $\omega_c$ that are computed from the same equivalent strain using two different damage functions $g_t$ and $g_c$. The $g_t$ is identified from the uniaxial tension tests, while $g_c$ from compressive test. The damage parameter for general stress states $\omega$ is obtained as a linear combination of $\omega_t$ and $\omega_c$: $\omega=\alpha_t g_t + \alpha_c g_c$, where the coefficients $\alpha_t$ and $\alpha_c$ take into account the character of the stress state. The damaged stiffness tensor is expressed as $D$$=(1-\omega)$$D$$^e$. Damage evolution law is postulated in an explicit form, relating damage parameter and scalar measure of largest reached strain level in material, taking into account the principle of preserving of fracture energy $G_f$. The equivalent strain, i.e., a scalar measure of the strain level is defined as norm from positive principal strains. The model description and parameters are summarized in Tab. 30.

Table 30: Mazars damage model - summary.

Description	Mazars damage model for concrete
Record Format	MazarsModel d(rn) # E(rn) # n(rn) # e0(rn) # ac(rn) # [bc(rn) #] [beta(rn) #] at(rn) # [ bt(rn) #] [hreft(rn) #] [hrefc(rn) #] [version(in) #] [tAlpha(rn) #] [equivstraintype(in) #] [maxOmega(rn) #]
Parameters	- num material model number
	- d material density
	- E Young modulus
	- n Poisson ratio
	- e0 max effective strain at peak
	- ac,bc material parameters related to the shape of uniaxial compression curve (A sample set used by Saouridis is $A_c = 1.34, B_c = 2537$
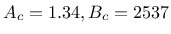	- beta coefficient reducing the effect of damage under response under shear. Default value set to 1.06
	- at, [bt] material parameters related to the shape of uniaxial tension curve. Meaning dependent on version parameter.
	- hreft, hrefc reference characteristic lengths for tension and compression. The material parameters are specified for element with these characteristic lengths. The current element then will have the same COD (Crack Opening Displacement) as reference one.
	- version Model variant. if 0 specified, the original form 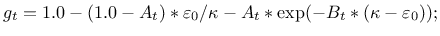$g_t= 1.0-(1.0-A_t)*\varepsilon_0/\kappa - A_t*\exp(-B_t*(\kappa-\varepsilon_0));$ of tension damage evolution law is used, if equal 1, the modified law used which asymptotically tends to zero $g_t = 1.0-(\varepsilon_0/\kappa)*\exp((\varepsilon_0-\kappa)/\varepsilon_f)$
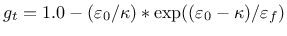	- tAlpha thermal dilatation coefficient
	- equivstraintype see Tab. 23
	- maxOmega limit maximum damage, use for convergency improvement
Supported modes	3dMat, PlaneStress, PlaneStrain, 1dMat