Nonlocal Mazars damage model for concrete - MazarsModelnl

The nonlocal variant of Mazars damage model for concrete. Model based on nonlocal averaging of equivalent strain. The nonlocal averaging acts as a powerful localization limiter. The bell-shaped nonlocal averaging function is used. The model description and parameters are summarized in Tab. 31.

Table 31: Nonlocal Mazars damage model - summary.

Description	Nonlocal Mazars damage model for concrete
Record Format	MazarsModelnl r(rn) # E(rn) # n(rn) # e0(rn) # ac(rn) # bc(rn) # beta(rn) # version(in) # at(rn) # [ bt(rn) #] r(rn) # tAlpha(rn) #
Parameters	- num material model number
	- d material density
	- E Young modulus
	- n Poisson ratio
	- maxOmega limit maximum damage, use for convergency improvement
	- tAlpha thermal dilatation coefficient
	- version Model variant. if 0 specified, the original form 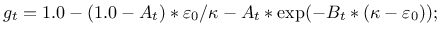$g_t= 1.0-(1.0-A_t)*\varepsilon_0/\kappa - A_t*\exp(-B_t*(\kappa-\varepsilon_0));$ of tension damage evolution law is used, if equal 1, the modified law used which asymptotically tends to zero $g_t = 1.0-(\varepsilon_0/\kappa)*\exp((\varepsilon_0-\kappa)/A_t)$
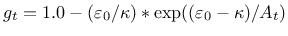	- ac,bc material parameters related to the shape of uniaxial compression curve (A sample set used by Saouridis is $A_c = 1.34, B_c = 2537$
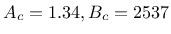	- at, [bt] material parameters related to the shape of uniaxial tension curve. Meaning dependent on version parameter.
	- beta coefficient reducing the effect of damage under response under shear. Default value set to 1.06
	- r parameter specifying the width of nonlocal averaging zone
Supported modes	3dMat, PlaneStress, PlaneStrain, 1dMat