| Description |
EC2CreepMat model for concrete creep and shrinkage |
| Record Format |
EC2CreepMat
n(rn) #
[ begOfTimeOfInterest(rn) #]
[ endOfTimeOfInterest(rn) #]
relMatAge(rn) #
[ timeFactor(rn) #]
stiffnessFactor(rn) #
[ tAlpha(rn) #]
fcm28(rn) #
t0(rn) #
cemType(in) #
[ henv(rn) #]
h0(rn) #
shType(in) #
[ spectrum ]
[ temperatureDependent ] |
| Parameters |
- num material model number |
| |
- n Poisson's ratio |
| |
- begOfTimeOfInterest determines the shortest time which is
reasonably well captured by the approximated compliance function (default
value is 0.1); the units are the time units of the analysis |
| |
- endOfTimeOfInterest determines the longest time which is
reasonably well captured by the approximated compliance function (if not
provided it is read from the engineering model); the units are the time units of the analysis |
| |
- relMatAge time shift used to specify the age of material on
the begging of the analysis, the meaning is the material age at time t =
0; |
| |
- timeFactor scaling factor transforming the actual time into
appropriate units needed by the formulae of the eurocode. For analysis
in days timeFactor = 1, for analysis in seconds timeFactor = 86,400. |
| |
- stiffnessFactor scaling factor transforming predicted
stiffness into appropriate units of the analysis, for analysis in MPa
stiffnessFactor = 1.e6 (default), for Pa stiffnessFactor = 1 |
| |
- fcm28 mean compressive strength measured on cylinders at
the age of 28 days in MPa |
| |
- t0 duration of curing [day] (this is relevant only for
drying shrinkage, not for creep) |
| |
- cemType type of cement, 1 = class R, 2 = class N, 3 = class
S |
| |
- henv ambient relative humidity expressed as decimal |
| |
- h0 effective member thickness in [mm] calculated according
to EC2 as 2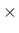 A/u where A is the cross-section are and u is the
cross-section perimeter exposed to drying A/u where A is the cross-section are and u is the
cross-section perimeter exposed to drying |
| |
- shType shrinkage type; 0 = no shrinkage, 1 = both drying
and autogenous shrinkage, 2 = drying shrinkage only, 3 = autogenous
shrinkage only |
| |
- spectrum this string switches on evaluation of the moduli
of the aging
Kelvin chain using the retardation spectrum of the compliance
function, otherwise (default option) the least-squares method is used |
| |
- temperatureDependent turns on the influence of temperature
on concrete maturity (equivalent age concept) by default this option is not activated. |
| Supported modes |
3dMat, PlaneStress, PlaneStrain, 1dMat,
2dPlateLayer,2dBeamLayer, 3dShellLayer |
![]() as
as
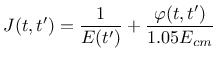
![]() (in days) is defined as
(in days) is defined as
![$\displaystyle E(t) = \left[ \exp \left( s \left(1-\sqrt{28/t} \right) \right)
\right]^{0.3} E_{cm}$](img441.png)
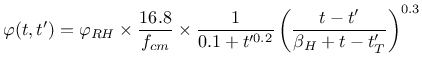
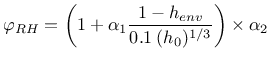
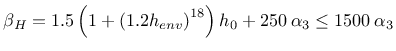
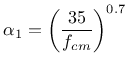
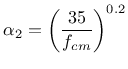
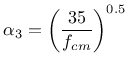
![]() and autogenous shrinkage
and autogenous shrinkage
![]() . Drying shrinkage strain at time
. Drying shrinkage strain at time ![]() is computed from
is computed from
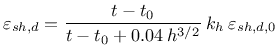
![$\displaystyle \varepsilon_{sh,a} = 2.5 \: (f_{cm} - 18) \left[ 1- \exp \left( -0.2 \sqrt{t} \right) \right] \times 10^{-6}$](img460.png)