Next: MPS damage model Up: Material models specific to Previous: Eurocode 2 model for
Model B3 is an aging viscoelastic model for concrete creep and shrinkage, developed by Prof. Bazant and coworkers. In OOFEM it is implemented in three different ways.
The first version, “B3mat”, is kept in OOFEM for compatibility. It is based on an aging Maxwell chain. The moduli of individual units in the chain are evaluated in each step using the least-squares method.
The second, more recent version, is referred to as “B3solidmat”. Depending on the specified input it exploits either a non-aging Kelvin chain combined with the solidification theory, or an aging Kelvin chain. It is extended to the so-called Microprestress-Solidification theory (MPS), which in this implementation takes into account only the effects of variable humidity on creep; the effects of temperature on creep are not considered. The underlying rheological chain consists of four serially coupled components. The solidifying Kelvin chain represents short-term creep; it is serially coupled with a non-aging elastic spring that reflects instantaneous deformation. Long-term creep is captured by an aging dashpot with viscosity dependent on the microprestress, the evolution of which is affected by changes of humidity. The last unit describes volumetric deformations (shrinkage and thermal strains). Drying creep is incorporated either by the “averaged cross-sectional approach”, or by the “point approach”.
The latest version is denoted as “MPS” and is based on the microprestress-solidification theory [28] [29] [30]. The rheological model consists of the same four components as in “B3solidmat”, but now the implemented exponential algorithm is designed especially for the solidifying Kelvin chain, which is a special case of an aging Kelvin chain. This model takes into account both humidity and temperature effects on creep. Drying creep is incorporated exclusively by the so-called
“point approach”. The model can operate in four modes,
controlled by the keyword
![]() . The first mode (
. The first mode (
![]() ) solves only the basic creep and runs as a single problem, while the remaining three modes need to be run as a staggered problem with humidity and/or temperature analysis preceding the mechanical problem; both humidity and temperature fields are read when
) solves only the basic creep and runs as a single problem, while the remaining three modes need to be run as a staggered problem with humidity and/or temperature analysis preceding the mechanical problem; both humidity and temperature fields are read when
![]() , only the field of relative humidity is taken into account when
, only the field of relative humidity is taken into account when
![]() and finally, only temperature when
and finally, only temperature when
![]() .
.
The basic creep is in the microprestress-solidification theory influenced by the same four parameters ![]() -
- ![]() as in the model B3. Values of these parameters can be estimated from the composition of concrete mixture and its compressive strength using the following empirical formulae:
as in the model B3. Values of these parameters can be estimated from the composition of concrete mixture and its compressive strength using the following empirical formulae:
| (105) | |||
| (106) | |||
| (107) | |||
| (108) |
The non-aging spring stiffness represents the asymptotic modulus of the material; it is equal to ![]() .
The solidifying Kelvin chain is composed of
.
The solidifying Kelvin chain is composed of ![]() Kelvin units with fixed retardation times
Kelvin units with fixed retardation times
![]() ,
,
![]() , which form a geometric progression with quotient 10. The lowest retardation time
, which form a geometric progression with quotient 10. The lowest retardation time ![]() is equal to
is equal to
![]() , the highest retardation time
, the highest retardation time ![]() is bigger than
is bigger than
![]() . The chain also contains a spring with stiffness
. The chain also contains a spring with stiffness
![]() (a special case of Kelvin unit with zero retardation time).
Moduli
(a special case of Kelvin unit with zero retardation time).
Moduli
![]() of individual Kelvin units are determined such that the chain
provides a good approximation of the non-aging micro-compliance function of the solidifying constituent,
of individual Kelvin units are determined such that the chain
provides a good approximation of the non-aging micro-compliance function of the solidifying constituent,
![]() , where
, where
![]() day and
day and ![]() .
The technique based on the continuous retardation spectrum
leads to the following formulae:
.
The technique based on the continuous retardation spectrum
leads to the following formulae:
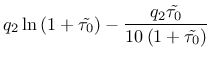 where where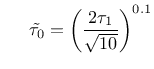 |
(109) | ||
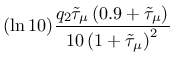 where where |
(110) |
The actual viscosities
![]() and stiffnesses
and stiffnesses ![]() of the solidifying chain change in time according to
of the solidifying chain change in time according to
![]() and
and
![]() , where
, where
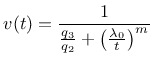 |
(111) |
Evolution of viscosity of the aging dashpot is governed by the differential equation
Equation (112) differs from the one presented in the original work; it replaces the differential equation for microprestress, which is not used here. The evolution of viscosity can be captured directly, without the need for microprestress. What matters is only the relative humidity and temperature and their rates. Parameters ![]() and
and ![]() of the original MPS theory
are replaced by
of the original MPS theory
are replaced by
![]() .
The initial value of viscosity is defined as
.
The initial value of viscosity is defined as
![]() ,
where
,
where ![]() is age of concrete at the onset drying or when the
temperature starts changing, in the present implementation it is set
is age of concrete at the onset drying or when the
temperature starts changing, in the present implementation it is set
![]() which corresponds to the material age when the material is cast.
which corresponds to the material age when the material is cast.
As mentioned above, under variable humidity and temperature conditions the physical time ![]() in function
in function ![]() describing evolution of the solidified volume is replaced by the equivalent time
describing evolution of the solidified volume is replaced by the equivalent time ![]() . In a similar spirit,
. In a similar spirit, ![]() is replaced by the solidification time
is replaced by the solidification time ![]() in the equation describing creep of the solidifying constituent, and by the reduced time
in the equation describing creep of the solidifying constituent, and by the reduced time ![]() in equation
d
in equation
d![]() d
d![]() relating the flow strain rate to the stress.
Factors transforming the physical time
relating the flow strain rate to the stress.
Factors transforming the physical time ![]() into
into ![]() ,
, ![]() and
and ![]() are defined as follows:
are defined as follows:
![$\displaystyle \exp \left[ \frac{Q_e}{R}\left( \frac{1}{T_0} - \frac{1}{T} \right) \right]$](img533.png) |
(117) | ||
![$\displaystyle \exp \left[ \frac{Q_r}{R}\left( \frac{1}{T_0} - \frac{1}{T} \right) \right]$](img535.png) |
(118) | ||
![$\displaystyle \exp \left[ \frac{Q_s}{R}\left( \frac{1}{T_0} - \frac{1}{T} \right) \right]$](img537.png) |
(119) |
![$\displaystyle \frac{1}{1+\left[\alpha_e \left( 1-h\right) \right]^4}$](img545.png) |
(120) | ||
| (121) | |||
| (122) |
At sealed conditions (or
![]() ) the auxiliary coefficients
) the auxiliary coefficients
![]() while at room temperature (or with
while at room temperature (or with
![]() ) factors
) factors
![]() .
.
It turned out that both the size effect on drying creep as well as its delay behind drying shrinkage can be addressed through parameter ![]() in the governing equation (112). In the experiments, the average (cross-sectional) drying creep is decreasing with specimen size. Unfortunately, for the standard value
in the governing equation (112). In the experiments, the average (cross-sectional) drying creep is decreasing with specimen size. Unfortunately, for the standard value ![]() , the MPS model exhibits the opposite trend. For
, the MPS model exhibits the opposite trend. For
![]() the size effect disappears, and for
the size effect disappears, and for ![]() it corresponds to the experiments. It should be noted that for negative or infinite values of
it corresponds to the experiments. It should be noted that for negative or infinite values of ![]() the underlying theory loses its original physical background.
If the experimental data of drying creep measured on different sizes
are missing, the exponent
the underlying theory loses its original physical background.
If the experimental data of drying creep measured on different sizes
are missing, the exponent
![]() can be taken as a realistic
estimate.
can be taken as a realistic
estimate.
When parameter ![]() is changed from its recommended value
is changed from its recommended value ![]() it is advantageous to rewrite the governing differential equation to the following form
it is advantageous to rewrite the governing differential equation to the following form
With the “standard value” ![]() (reverted size effect) the new
parameter
(reverted size effect) the new
parameter ![]() is also 2, for
is also 2, for ![]() (correct size effect)
(correct size effect)
![]() and finally with
and finally with
![]() the first parameter
the first parameter
![]() and the second parameter
and the second parameter ![]() becomes
dimensionless. The other advantage of
becomes
dimensionless. The other advantage of
![]() is that the
governing differential equation becomes linear and can be solved
directly.
is that the
governing differential equation becomes linear and can be solved
directly.
The rate of thermal strain is expressed as
![]() and the rate of drying shrinkage strain as
and the rate of drying shrinkage strain as
![]() , where both
, where both ![]() and
and ![]() are assumed to be constant in time and independent of temperature and humidity.
are assumed to be constant in time and independent of temperature and humidity.
There are two options to simulate the autogenous shrinkage in the MPS material model. The first one is according to the B4 model
For the normally hardening cement, the ultimate value of the autogenous shrinkage can be estimated from the composition using the empirical formula of the B4 model
Similarly, in the Model Code, the ultimate shrinkage strain can be estimated from the mean concrete strength at the age of 28 days and from the cement grade
The model description and parameters are summarized
in Tab. 35 for “B3mat”, in Tab. 36 for “B3solidmat”, and in Tab. 37 for “MPS”.
Since some model parameters are determined from the composition
and strength using empirical formulae, it is necessary to use the
specified units (e.g. compressive strength always in MPa, irrespectively
of the units used in the simulation for stress).
For “B3mat” and “B3solidmat” it is strictly
required to use the specified units in the material input record (stress always in MPa, time in days etc.).
The “MPS” model is almost unit-independent, except for
![]() in MPa and
in MPa and ![]() in kg/m
in kg/m![]() , which are used in empirical formulae.
, which are used in empirical formulae.
For illustration, sample input records for the material considered in Example 3.1 of the creep
book by Bazant and Jirásek is presented. The concrete mix is composed
of 170 kg/m![]() of water, 450 kg/m
of water, 450 kg/m![]() of type-I cement and 1800 kg/m
of type-I cement and 1800 kg/m![]() of aggregates,
which corresponds to ratios
of aggregates,
which corresponds to ratios
![]() and
and ![]() . The compressive strength
is
. The compressive strength
is
![]() MPa. The concrete slab of thickness 200 mm is cured in air
with initial protection against drying until the age of 7 days.
Subsequently, the slab is exposed to an environment with
relative humidity of 70%. The following input record can be used for the first
version of the model (B3mat):
MPa. The concrete slab of thickness 200 mm is cured in air
with initial protection against drying until the age of 7 days.
Subsequently, the slab is exposed to an environment with
relative humidity of 70%. The following input record can be used for the first
version of the model (B3mat):
B3mat 1 n 0.2 d 0. talpha 1.2e-5 relMatAge 28. fc 45.4 cc 450. w/c 0.3778 a/c 4. t0 7. timefactor 1. alpha1 1. alpha2 1.2 ks 1. hum 0.7 vs 0.1 shmode 1
Parameter
![]() corresponds to type-I cement, parameter
corresponds to type-I cement, parameter
![]() to curing in air, parameter
to curing in air, parameter ![]() to an infinite slab.
The volume-to-surface ratio is in this case
equal to one half of the slab thickness
and must be specified in meters, independently of the length units that are
used in the finite element analysis (e.g., for nodal coordinates).
The value of relMatAge must be specified in days.
Parameter relMatAge 28. means that time 0
of the analysis corresponds to concrete age 28 days.
If material B3mat is used, the finite element analysis
must use days as the units of time (not only for relMatAge,
but in general, e.g. for the time increments).
to an infinite slab.
The volume-to-surface ratio is in this case
equal to one half of the slab thickness
and must be specified in meters, independently of the length units that are
used in the finite element analysis (e.g., for nodal coordinates).
The value of relMatAge must be specified in days.
Parameter relMatAge 28. means that time 0
of the analysis corresponds to concrete age 28 days.
If material B3mat is used, the finite element analysis
must use days as the units of time (not only for relMatAge,
but in general, e.g. for the time increments).
If only the basic creep (without shrinkage) should be computed, then the material input record reduces to following: B3mat 1 n 0.2 d 0. talpha 1.2e-5 relMatAge 28. fc 45.4 cc 450. w/c 0.3778 a/c 4. t0 7. timefactor 1. shmode 0
| Description | B3solid material model for concrete creep |
| Record Format | B3solidmat d(rn) # n(rn) # talpha(rn) # mode(in) # [ EmoduliMode(in) #] Microprestress(in) # shm(in) # [ begoftimeofinterest(rn) #] [ endoftimeofinterest(rn) #] timefactor(rn) # relMatAge(rn) # fc(rn) # cc(rn) # w/c(rn) # a/c(rn) # t0(rn) # q1(rn) # q2(rn) # q3(rn) # q4(rn) # c0(rn) # c1(rn) # tS0(rn) # w_h(rn) # ncoeff(rn) # a(rn) # ks(rn) # [ alpha1(rn) #] [ alpha2(rn) #] hum(rn) # vs(rn) # q5(rn) # kt(rn) # EpsSinf(rn) # es0(rn) # r(rn) # rprime(rn) # at(rn) # kSh(rn) # inithum(rn) # finalhum(rn) # |
| Parameters | - num material model number |
| - d material density | |
| - n Poisson ratio | |
| - talpha coefficient of thermal expansion | |
| - mode optional parameter; if |
|
| - EmoduliMode optional parameter; analysis of retardation spectrum ( |
|
| - Microprestress |
|
| - shmode shrinkage mode;
|
|
| - begoftimeofinterest optional parameter; lower boundary of time interval with good approximation of the compliance function [day]; default 0.1 day | |
| - endoftimeofinterest optional parameter; upper boundary of time interval with good approximation of the compliance function [day] | |
| - timefactor scaling factor transforming the simulation time units into days | |
| - relMatAge relative material age [day] |
|
Now consider the same conditions for “B3solidmat”.
In all the examples below,
the input record with the material description can start by
B3solidmat 1 d 2420. n 0.2 talpha 12.e-6 begtimeofinterest 1.e-2
endtimeofinterest 3.e4 timefactor 86400. relMatAge 28.
Parameters begoftimeofinterest 1.e-2 and endoftimeofinterest 3.e4 mean that the computed response (e.g., deflection) should be accurate in the range from 0.01 day to 30,000 days after load application. Parameter timefactor 86400. means that the time unit used in the finite element analysis is 1 second (because 1 day = 86,400 seconds). Note that the values of begtimeofinterest, endtimeofinterest and relMatAge are always specified in days, independently of the actual time units in the analysis. Parameter EmoduliMode is not specified, which means that the moduli of the Kelvin chain will be determined using the default method, based on the continuous retardation spectrum.
Additional parameters depend on the specific type of analysis:
| Description | Microprestress-solidification theory material model for concrete creep |
| Record Format | mps d(rn) # n(rn) # talpha(rn) # referencetemperature(rn) # mode(in) # [ CoupledAnalysisType(in) #] [ begoftimeofinterest(rn) #] [ endoftimeofinterest(rn) #] timefactor(rn) # relMatAge(rn) # lambda0(rn) # fc(rn) # cc(rn) # w/c(rn) # a/c(rn) # stiffnessfactor(rn) # q1(rn) # q2(rn) # q3(rn) # q4(rn) # ksh(rn) # [ mus(rn) #] k3(rn) # [ alphaE(rn) #] [ alphaR(rn) #] [ alphaS(rn) #] [ QEtoR(rn) #] [ QRtoR(rn) #] [ QStoR(rn) #] kTm(rn) # [ kTc(rn) #] [ p(rn) #] [ p_tilde(rn) #] [ alpha_as(rn) #] [ eps_cas0(rn) #] [ b4_eps_au_infty(rn) #] [ b4_tau_au(rn) #] [ b4_alpha(rn) #] [ b4_r_t(rn) #] [ b4_cem_type(rn) #] [ temperInCelsius ] |
| Parameters | - num material model number |
| - d material density | |
| - n Poisson ratio | |
| - talpha coefficient of thermal expansion | |
| - referencetemperature reference temperature only to thermal expansion of material | |
| - mode optional parameter; if |
|
| - CoupledAnalysisType |
|
| - lambda0 scaling factor equal to 1.0 day in time units of analysis (e.g. 86400 if the analysis runs in seconds) | |
| - begoftimeofinterest lower boundary of time interval with good approximation of the compliance function; default value = 0.01 |
|
| - endoftimeofinterest upper boundary of time interval with good approximation of the compliance function; default value = 10000. |
|
| - timefactor scaling factor, for mps material must be equal to 1.0 | |
| - relMatAge relative material age = age at time when the material is cast in the structure |
|
Finally consider the same conditions for “MPS material”.
In all the examples below,
the input record with the material description can start by
mps 1 d 2420. n 0.2 talpha 12.e-6 referencetemperature 296.
Additional parameters depend on the specific type of analysis:
Final recommendations:
Borek Patzak