Next: Microplane model M4 - Up: Material models specific to Previous: B3 and MPS models
This model extends the model based on the Microprestress-Solidification theory, described in previous section and summarized in Tab. 37 for “MPS”, by tensile cracking.
This extension uses the isotropic damage model with Rankine definition of the equivalent deformation defined as the biggest principal effective stress divided by the elastic modulus. The softening law cannot deal directly with the strain because due to creep strain increases and this would lead to further softening without additional loading.
Two different approaches are implemented. The first one, default, (#1) reduces the stiffness only in the directions of tension (in case the tensile strength is exceeded). A full stiffness is restored in compression and after unloading from tension.
The other approach (#2) is the standard isotropic damage model which reduces the stiffness equally in all directions independently of loading. This approach leads to faster convergence because the secant stiffness can be used instead of the incremental viscoelastic stiffness which must be used in the first approach. The second approach becomes useful when the loading is monotonic or when the benefit of the accelerated computation prevails over the consequences of the reduced/underestimated stiffness in compression.
Proper energy dissipation is guaranteed by the crack-band approach.
The following algorithm is used to compute the stress vector (in each time step and until the iteration criteria are met):
| (130) |
| (131) |
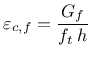 |
(132) |
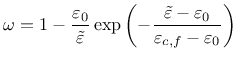 |
(133) |
| (134) |
The tensile strength and fracture energy can be defined either as fixed, time-independent values (parameters ![]() ,
, ![]() ) or as variable, depending on the equivalent hydration time
) or as variable, depending on the equivalent hydration time ![]() . The latter case is activated by keyword
. The latter case is activated by keyword
![]() ; tensile strength and fracture energy are then linked to the current value of the mean compressive strength using (slightly modified) formulae from the fib Model Code 2010.
; tensile strength and fracture energy are then linked to the current value of the mean compressive strength using (slightly modified) formulae from the fib Model Code 2010.
For
![]() MPa the tensile
strength is computed from a linear function
MPa the tensile
strength is computed from a linear function
| (135) |
| (136) |
| (137) |
Following the guidelines from the Model Code 2010 (section 5.1.5.2),
the fracture energy ![]() can be estimated from the mean compressive
strength at 28 days using an empirical formula
can be estimated from the mean compressive
strength at 28 days using an empirical formula
The growth in fracture energy is approximately proportional to the tensile strength. The current value of fracture energy is very simply computed as
The development of the mean compressive strength in time is adopted entirely from the Model Code 2010 (see section 5.1.9.1)
For some concretes the prediction formulae do not provide accurate predictions, therefore it is possible to scale the evolution of tensile strength and fracture energy by providing their 28-day values ft28 and gf28.
The model description and parameters are summarized in Tab. 38.
|
Borek Patzak