| Description |
Nonlinear isotropic material for moisture transport |
| Record Format |
BazantNajjarMoistureMat num(in) #
d(rn) # c1(rn) # n(rn) #
alpha0(rn) # hc(rn) # [ capa(rn) #] |
| Parameters |
- num material model number |
| |
- d material density |
| |
- c1 moisture diffusivity at full saturation [m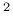 s s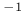 ] ] |
| |
- n exponent [-] |
| |
- alpha0 ratio between minimum and maximum diffusivity [-] |
| |
- hc relative humidity at which the diffusivity is exactly
between its minimum and maximum value [-] |
| |
- capa moisture capacity (default value is 1.0) |
| Supported modes |
_2dHeat |