Multiscale Simulation of Fracturing of Carbon-epoxy Braided composites
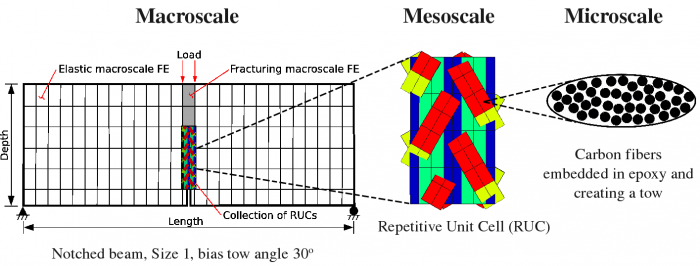
Two-dimensional triaxially braided composites (2DTBCs) can dissipate large amount of energy during fracturing. The biggest challenge remains in engineering this carbon-epoxy composite to optimize energy dissipation and to discover critical and sensitive factors affecting fracturing performance. The simulation started with the definition and dicretization of Repetitive Unit Cell (RUC), see Figure below
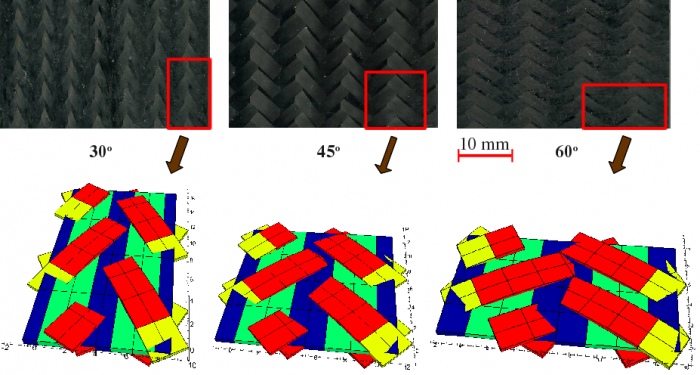 |
| Images of 2DTBC and reconstructed RUCs with bias tow angles of 30o, 45o and 60o. SEM images from University of Michigan, prof. Waas' group. |
Since the fracture parameters are best manifested in the scaling properties of the size effect law, the nominal strengths of three geometrically self-similar notched beams are simulated in a 3D finite element framework. A collection of RUCs is embeded above the notch while the rest of beam has coarse finite elements, see Figure. Python script helped to generate the embedded geometry using hanging nodes and master-slave node relation.
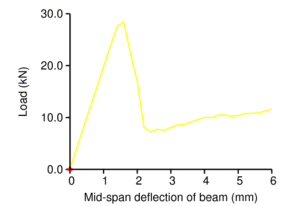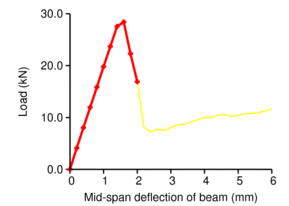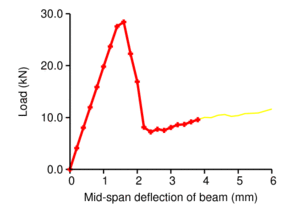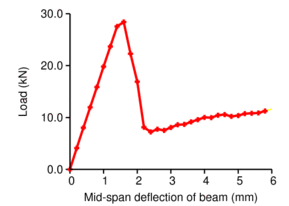
The simulation stems from damage mechanics. A fixed orientation of three perpendicular planes, aligned with material orientation axes, defines six damage variables; three for normal stress and three for shear. The OOFEM class CompoDamageMat handles such damage material. The left Figure shows the notched beam with embedded damaging RUCs, the right Figure displays the force-displacement curve.
The Figure below depicts a detailed view of the process zone above the notch. The colors represent damage magnitude on carbon axial and bias tows.
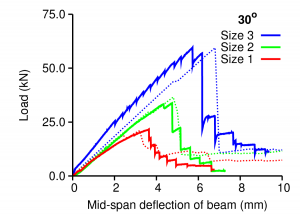
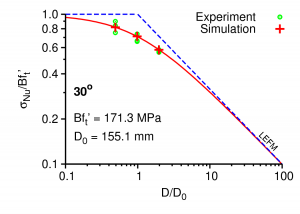
The left Figure shows a detail of the three-point beam bending test, the middle Figure prediction and simulation for three beam sizes, and the right Figure fitting to the the size effect law.
By fitting the size effect law, the fracture energy was found in the range 212 - 464 N/mm. For more information, see our article
- V. Šmilauer, C. G. Hoover, Z. P. Bažant, F. C. Caner, A. M. Waas, K. W. Shahwan: Multiscale Simulation of Fracture of Braided Composites via Repetitive Unit Cells, Engineering Fracture Mechanics, 78(6), 901-918. ISSN 0013-7944, 2011.
Created 12/2010 by Vít Šmilauer. Acknowledgements belong also to C. G. Hoover, B. Patzák, Z. P. Bažant, A. M. Waas and K. W. Shahwan.