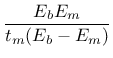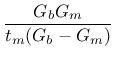Masonry is a composite material made of bricks and mortar. Nonlinear behavior of both components should be considered to obtain a realistic model able to describe cracking, slip, and crushing of the material. The model is based on paper by Lourenco and Rots [17]. It is formulated on the basis of softening plasticity for tension, shear, and compression (see fig.(1)). Numerical implementation is based on modern algorithmic concepts such as implicit integration of the rate equations and consistent tangent stiffness matrices.
Figure 1:
Composite yield surface model for masonry
|
|
The approach used in this work is based on idea of concentrating all the damage in the relatively weak joints and, if necessary, in potential tension cracks in the bricks. The joint interface constitutive model should include all important damage mechanisms. Here, the concept of interface elements is used. An interface element allows to incorporate discontinuities in the displacement field and its behavior is described in terms of a relation between the tractions and relative displacement across the interface. In the present work, these quantities will be denoted as
 , generalized stress, and
, generalized stress, and
 , generalized strain. For 2D configuration,
, generalized strain. For 2D configuration,
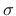
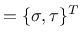 and
and
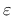
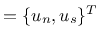 , where
, where 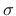 and
and 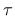 are the normal and shear components of the traction interface vector and
are the normal and shear components of the traction interface vector and 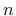 and
and 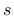 subscripts distinguish between normal and shear components of displacement vector.
subscripts distinguish between normal and shear components of displacement vector.
Figure 2:
Modeling strategy for masonry
|
|
The elastic response is characterized in terms of elastic constitutive matrix
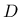 as
as
For a 2D configuration
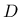
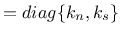 . The terms of the elastic stiffness matrix can be obtained from the properties of both masonry and joints as
. The terms of the elastic stiffness matrix can be obtained from the properties of both masonry and joints as
where 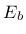 and
and 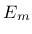 are Young's moduli,
are Young's moduli, 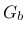 and
and 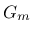 shear moduli for brick and mortar, and
shear moduli for brick and mortar, and 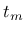 is the thickness of joint. One should note, that there is no contact algorithm assumed between bricks, this means that the overlap of neighboring units will be visible. On the other hand, the interface model includes a compressive cap, where the compressive inelastic behavior of masonry is lumped.
is the thickness of joint. One should note, that there is no contact algorithm assumed between bricks, this means that the overlap of neighboring units will be visible. On the other hand, the interface model includes a compressive cap, where the compressive inelastic behavior of masonry is lumped.
Subsections
Borek Patzak
2019-03-19
![]() , generalized stress, and
, generalized stress, and
![]() , generalized strain. For 2D configuration,
, generalized strain. For 2D configuration,
![]()
![]() and
and
![]()
![]() , where
, where ![]() and
and ![]() are the normal and shear components of the traction interface vector and
are the normal and shear components of the traction interface vector and ![]() and
and ![]() subscripts distinguish between normal and shear components of displacement vector.
subscripts distinguish between normal and shear components of displacement vector.