For the shear mode a Coulomb friction envelope is used. The yield function has the form
According to [17] the variations of friction angle 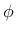 and cohesion
and cohesion 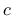 are assumed as
are assumed as
where 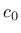 is initial cohesion of joint,
is initial cohesion of joint, 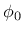 initial friction angle,
initial friction angle, 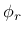 residual friction angle, and
residual friction angle, and 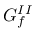 fracture energy in mode II failure. A non-associated plastic potential
fracture energy in mode II failure. A non-associated plastic potential 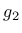 is considered as
is considered as
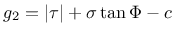 |
(62) |
Figure:
Shear behavior of proposed model for different confinement levels in MPa (
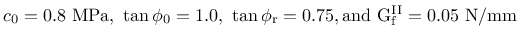 )
)
|
|
Borek Patzak
2019-03-19