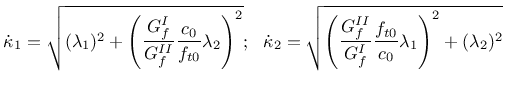Coupling of tension/shear modes

The tension and Coulomb friction modes are coupled with isotropic softening. This means that the percentage of softening in the cohesion is assumed to be the same as on the tensile strength

$\displaystyle \dot\kappa_1=\lambda_1+$ $\displaystyle \mbox{$\displaystyle\frac{G^I_f}{G^{II}_f}$}$ $\displaystyle \mbox{$\displaystyle\frac{c_0}{f_{t0}}$}$ $\displaystyle \lambda_2;\ \ \dot\kappa_2=$ $\displaystyle \mbox{$\displaystyle\frac{G^{II}_f}{G^I_f}$}$ $\displaystyle \mbox{$\displaystyle\frac{f_{t0}}{c_0}$}$ $\displaystyle \lambda_1+\lambda_2$

(63)

This follows from (58) and (60). However, in the corner region, when both yield surfaces are activated, such approach will lead to a non-acceptable penalty. For this reason a quadratic combination is assumed

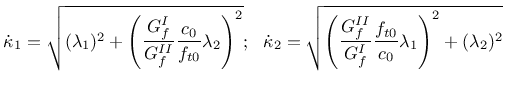$\displaystyle \dot\kappa_1=\sqrt{(\lambda_1)^2+\left(\mbox{$\displaystyle\frac{... ...I_f}$}\mbox{$\displaystyle\frac{f_{t0}}{c_0}$}\lambda_1\right)^2+(\lambda_2)^2}$

(64)

Borek Patzak
2019-03-19